最近(2012年1月)、内閣府は「経済財政に関する中長期試算」を公表した。
この試算(慎重シナリオ)によると、一体改革が失敗して消費税が5%で推移した場合、2020年度の基礎的財政収支(対GDP)は4%の赤字となる。
他方、社会保障・税一体改革が成功して消費税が10%に引き上がった場合、2020年度の基礎的財政収支(対GDP)は3%の赤字となると試算している。
一体改革が成功すると、2020年度の基礎的財政収支(対GDP)は1%改善するとの試算であるが、それでも3%もの赤字が継続する。これは一体改革は「止血剤」に過ぎず、さらに大幅な増税や社会保障削減が不可欠であることを意味する。
だが、「経済成長のみで財政再建は可能である」との意見がいまだに存在する。
これが不可能であることは、拙著『2020年、日本が破綻する日』や『日本破綻を防ぐ2つのプラン』で詳しく説明しているが、今回は若干異なる視点で説明してみよう(厳密には「動学的効率性」に関する議論が必要であるが、専門的な知識が必要なため、ここでは議論しない)。
このため、公的債務(対GDP)の変化を示す以下の「ドーマー条件」を考える。
公的債務(対GDP)の変化=-基礎的財政収支(対GDP)+(金利-成長率)×現在の公的債務(対GDP)
ここでの「金利」は「国債利回り(長期金利)」を意味するが、左辺の「公的債務(対GDP)」に「0(ゼロ)」を代入し、右辺の「基礎的財政収支(対GDP)」に中長期試算の▲4%、「現在の公的債務(対GDP)」に「200%」を代入した上で、X=成長率-金利と置き、Xを求めてみよう。
答えは簡単で、X=2%が導かれる。これは、成長率が金利よりも2%以上高い場合、経済成長のみで財政再建が可能であることを意味する。
つまり、金利が現在の長期金利(1%前後)である場合、成長率が3%以上であれば、増税無しの経済成長のみで財政再建は可能となる。なお、「現在の公的債務(対GDP)」を「100%」とする場合、X=4%となり、金利=1%での成長率は5%以上となる。
では、「現在の公的債務(対GDP)=200%」の場合、X=2%であり、成長率が金利よりも2%以上も高くなる確率はどの程度であろうか。
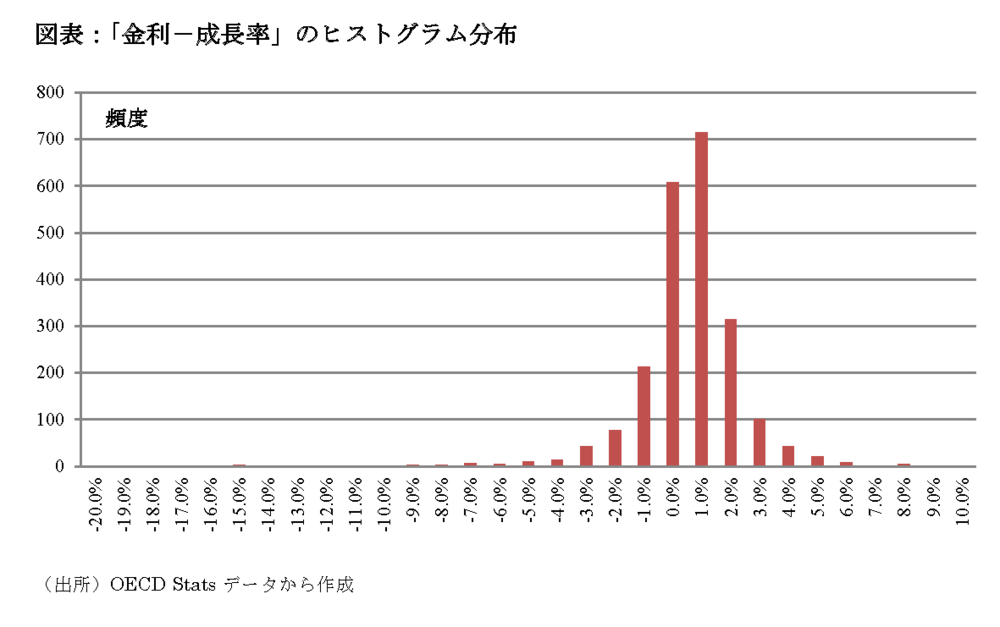
「成長率(名目)」と「長期金利(名目)」に関するOECDデータから、「金利-成長率」のヒストグラム分布を作成してみたのが、以下の図表である。
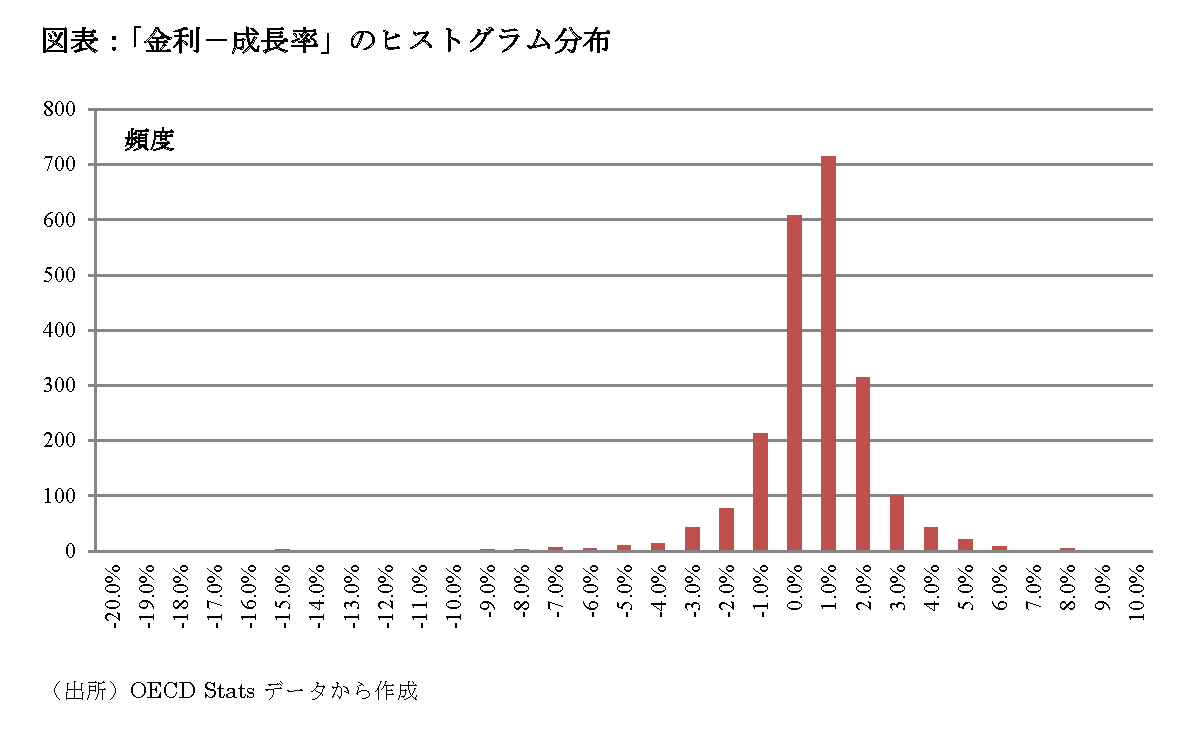
この図表からは、「金利>成長率」の頻度の方が多いことが読み取れる。その際、「金利-成長率≦-2%」となる割合は、全体のサンプル数=2195個のうち165個の7.6%に過ぎない。
しかも、これは単年での確率である。経済成長のみで財政再建を行うためには、毎年、「金利-成長率≦-2%」を達成する必要がある。この確率は、2年間連続で7.6%×7.6%=0.57%になる。当たり前であるが、10年間連続では7.6%の10乗であるから、概ねゼロに近い。
(一橋大学経済研究所准教授 小黒一正)