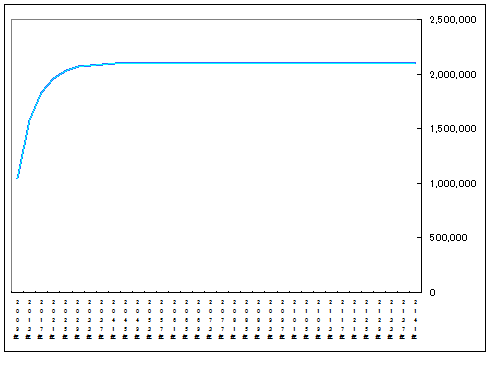
ビットコインの発行量は、上限が2100万枚と設定されている。徐々に発行されていくようなイメージをもつ人もいるが、そうではない。最初に、急激に発行され、その後は極端に発行量が減る。
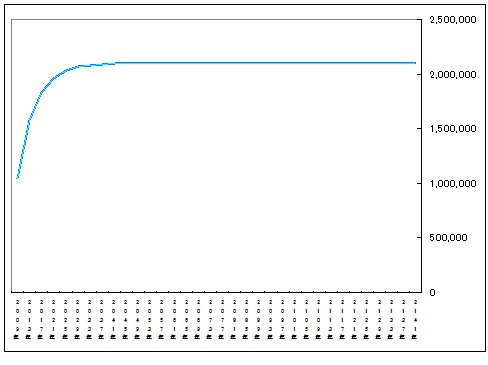
#グラフの目盛りに間違いがありました。本来より一桁少なくなっておりますが、グラフの曲線自体は正しいものですので、このままに致します。
2017年には総量の87.5%、2033年には、99%のコインが発行されてしまう。のこり108年かけて、わずか1%のコインが微妙に発行されるに過ぎない。
これは、コイン発行の規則による。4年毎に発行量が半減するという規則だ。これは(1/2)^nという指数関数になるので、当初はたくさん発行されるが時間が少したつだけで発行量が極度に減る。
グラフをみても、急激にフラットになっているのがわかる。2033年あたりから完全にフラットだ。
そして、発行総量は2100万枚という上限(極限)に限りなく近づいていくが、決して2100万枚を超えることはない*1。
このような発行方式の問題点を指摘する人も多い。急速に発行量がへるので、初期に手に入れたマイナーの先行者利益が大きすぎる。また発行上限は決して2100万枚を超えることがないので、コインの総量が増えずに、デフレ経済になるというのが主なものだ。
これに対して、フェイスブックの仮想通貨のコミュニティで、近畿大の山崎先生が「素数分の1で減っていく仕組みが良いのでは」とつぶやいていたので、実際にグラフを書いてみた。
素数分の1とは、発行量が、1/2, 1/3, 1/5, 1/7, 1/11, 1/13と、素数を順番に分母にして減っていくという仕組みである。これなら、なだらかに減っていく。
しかしながら、素数分の1の数を足していくと、じつは無限大になる。長い時間を取れば、コインの発行総量はいくらでも多くなるのだ。(数学的にいうと数列が「発散」するという)。つまり、発行の上限がないということ。
つまり、次第に減っていく特徴は一緒としても、発行の上限がない。いくらでも発行される。なかなかおもしろいと思う。
実際に素数分の1のグラフを書いてみた。
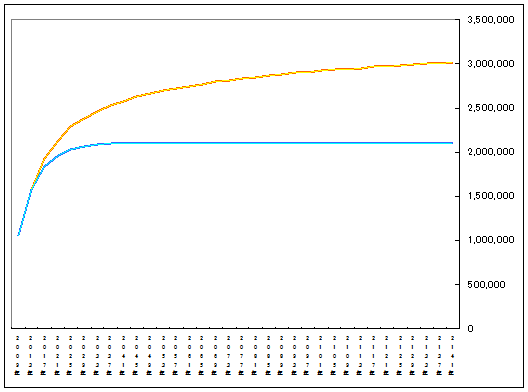
オレンジ色が素数分の1のグラフ: Σ [1/p(n)]
青色が、半減のグラフ : Σ [(1/2)^n]
これを見るとわかるように、青線が急激に2100万コインにちかづいて、その後平坦になってしまうのに対して、オレンジの線は、そこそこのペースで増え続けていることがわかる。
2140年頃には、青線が2100万枚にたいして、オレンジは3000万枚だ。
なにより素数にはロマンがある。こういう発行方式をとったコインが現れてもいいかもしれない。
*1 ビットコインの発行量の総数は以下の式で求められる。210,000ブロックごとに半減で、1ブロックあたり50BTCが当初の量だから。
210,000 block * 50 * (1 + 1/2 + 1/4 + 1/8 ・・・) 括弧内の無限和の極限は2になる。
=210,000 * 50 * 2
= 210,000 *100
= 21,000,000