高梨沙羅ちゃん、団体でも不幸に見舞われ痛々しい限り。ノーマルヒルの結果に関して、日経新聞の記事に「風の運・飛型点、個人戦の敗因に」という見出しでこう書かれていた。
風の向きや強さに応じて「ウインドファクター」で点は加減されるものの、風を利して飛距離を稼いだ方が点が伸びやすい。
確かにスキーのジャンプにおいては、選手の跳躍の毎に風速が変化しそれが飛距離に影響を与える。しかし「風の運」で勝敗、もしくはメダルの色や獲得の有無が決まってしまうとなれば、スポーツにギャンブルの要素が入り込んでいるようなものであろう。記事の雰囲気は「どんなスポーツや勝負でも運不運はつきもの」と一言で片づけているようにも読める。
実際スキージャンプにおいては、風速の変化という選手には抗い難い自然の影響が他のどんなスポーツより大きいという事実は認識されている。「ウインドファクター」という風速の影響を補正する要素があり、最終的なジャンプの得点計算で調整されている。
では「ウインドファクター」の実態はどんなものなのか? 風速の影響を公平に反映しているのか?というのが本論の考察である。

technotr/iStock
データの出典は、北京五輪の結果の詳細を公開している「gorin.jp」というページ(スキージャンプ女子ノーマルヒル|gorin.jp 民放オリンピック公式動画サイト)から。ノーマルヒル女子のデータからジャンプ能力が同等と思われるトップの5人のデータを用いた。オリジナルの記載は見にくいので筆者のまとめたデータが下表である。
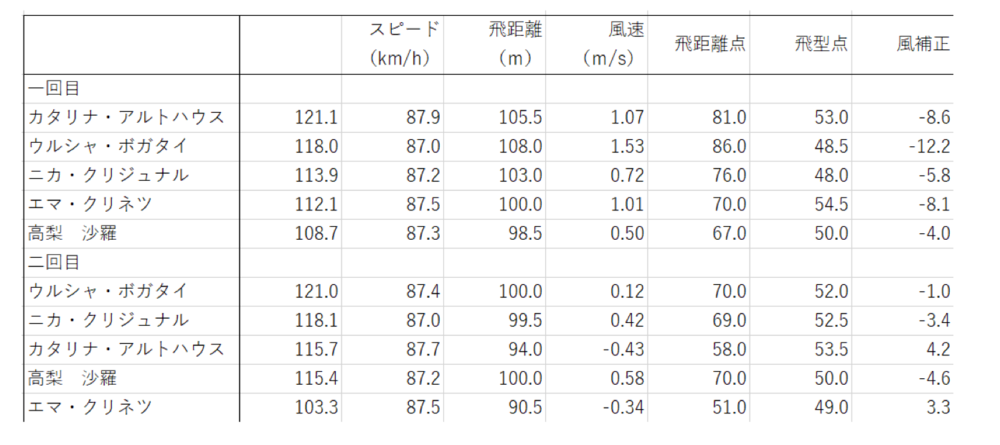
一回のジャンプ得点は、簡単に書けば、飛距離から算出される飛距離点と飛形点、風の補正点=ウインドファクターの合計となる。それらの点数の重みというか構成を見たのが下図。上の表の10回のジャンプの平均点を採った。
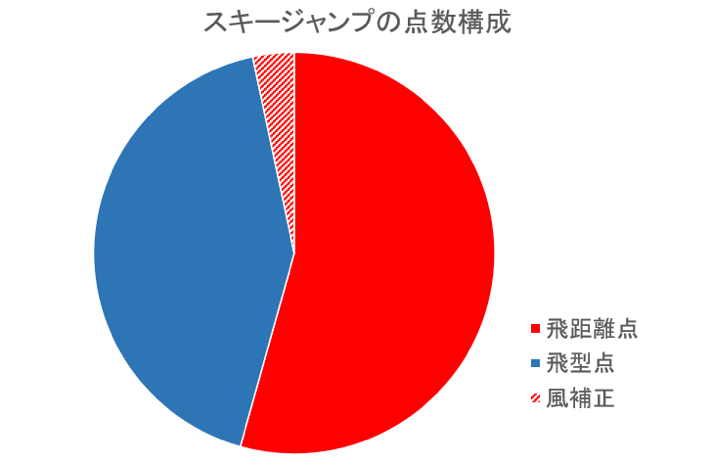
ノーマルヒルの女子では総得点の約6割が飛距離、4割が飛形点、ウインドファクターは約3%(マイナスの場合は飛距離から差し引かれる)だった。意外と飛形点の重みが大きいが、標準偏差は小さく、標準偏差が大きいのは飛距離点であるから、やはり勝負は飛距離によって概ね決まると考えてよさそうだ。
スキーのジャンプでは向かい風の方が浮力を増すので飛距離が伸びる。逆に追い風だと浮力が落ち飛距離は伸びない。では実際に風の影響は定量的にどれほどなのか?これが本論の最大の関心事項であった。
今回の5名、全員が100メートルを飛んでおり、踏切時の速度は最低時速87.0キロから最高87.9キロと平均値との差は0.5%もなく、ジャンプ能力に大差はないとみて良い。
そこで各自の一回目と二回目のジャンプを風速と飛距離平面にて較べた。結果は5名全員が、向かい風が強いほど飛距離が伸びていた。しかもその角度、すなわち風速の飛距離に与える影響はほぼ同じレベルであった。このデータは各選手において飛ぶごとに出来不出来があるわけではなく、全員がたぶん毎回安定したジャンプをしているということでもある。その論理的帰結は、飛距離の差の主たる要因は風速差である、ということである。
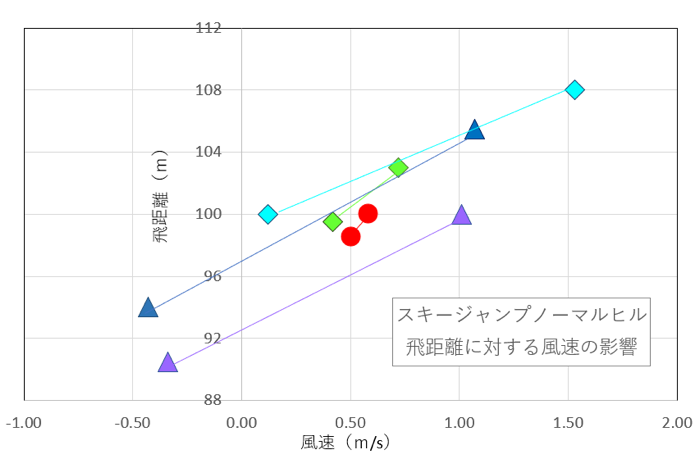
そこで風速の飛距離に対する影響を直線で近似した(下図)。結果は風速1メートルの向かい風に対して、飛距離は7.5メートル延びるというものだった。追い風、すなわち風速がマイナスであるとK点の95メートルに達することもできない。いい例が一回目トップのアルトハウス(青▲)で、追い風となった二回目は94メートルだった。
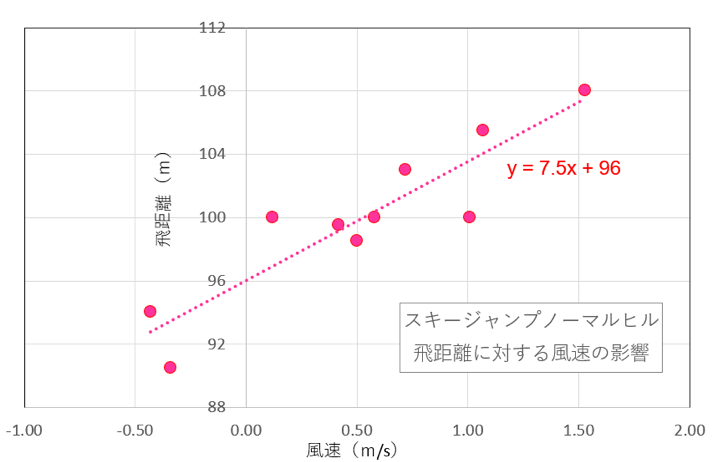
そこでウインドファクターが登場する。風の運、不運を調整し点数の公正を担保するという趣旨で導入されたのであろう。まずウインドファクターがどのようにして算出されるのか不明であったため、それを推定した。風速とウインドファクターをプロットすると単純な直線になったことから風速に約8.35を掛けて求めているようだ。近似曲線が風速0でほぼ0点なので大過はないだろう。すなわち風速1メートルにつき8.35点飛距離点を補正される。これがウインドファクター=風補正点。
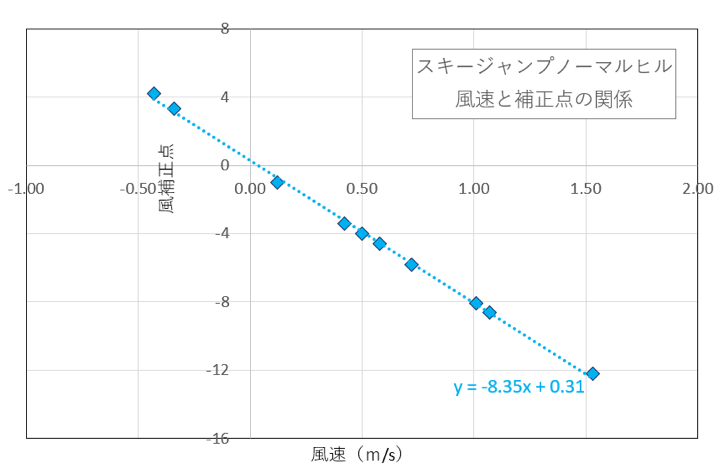
次に飛距離点、これは単純でK点(95メートル)を基準の60点とし、飛距離が1メートルに付き2点プラスマイナスされる。冒頭の表を見れば明らか。先に、「風速1メートルの向かい風に対して、飛飛距離は7.5メートル延びる」ことが判った。点数にすると15点増えるということである。
ということは、風速の影響を公正に得点に反映するためには、風速に対する補正としての現行のウインドファクターの算出係数8.35は非現実的、実態からはウインドファクターの算出係数は15.0でなければないことを意味している。
今回のノーマルヒルのジャンプの飛距離に対し、風補正点の差をプロットしたのが下図。ある選手が1.5メートルの向かい風に出会ったとしよう。飛距離増のメリットが大きく、現ウインドファクターの調整点より11点ほど得をする。風の強さ(風速、風向)によるメリットがメダルの有無や色の差になっている。スポーツの仮面をかぶったギャンブル、といってもいいぐらい。
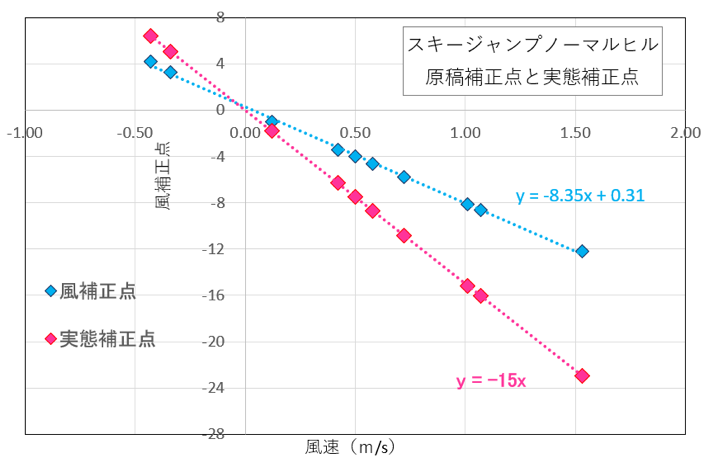
今回得た15.0という数字は一競技から得た仮の値でサンプル数は少ないが、関係団体の保有する膨大なデータを統計処理すればより正確な値を得られるだろう。ただし値に大きな差は生じないはずだ。こんな不公平なシステムが公認されているとは驚きであった。関係者は誰も異議を唱えないのであろうか。














