今回の自粛による膨大な経済的損失はコロナによる直接の損害ではなく、「ヒトとの接触8割削減をしないと42万人死亡」という予測をもとに施行された疫学的予防措置によるものです。この措置の妥当性は厳しく検証されるべきものです。

自粛期間中、平日昼も人気が消えていた銀座(編集部撮影)
アゴラで山本民次氏が述べておられるように、当初の予測モデルの検証が、データがだいぶ更新された現在でもあまり出てこないことは、分野は違いますがシミュレーションコードの開発とそれを用いた評価業務を行っているものとしては甚だ不満です。そこで自粛の効果をPHITSというモンテカルロシミュレーションコードを用いて検証してみました。
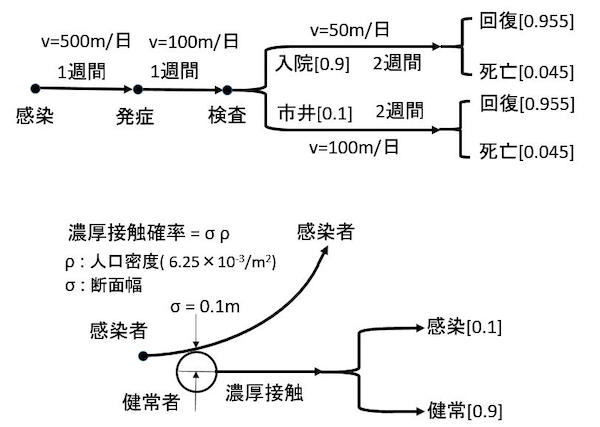
シミュレーションに取り込んだプロセスは図1のような単純なものです。感染した人は1週間で発症し、更に1週間で検査を受け入院するか、そのまま市井にいるか決まります。いずれの場合もそこから2週間で回復するか死亡します。回復した人が免疫を獲得して次の感染はしないという効果は考慮されていません。
これらの期間は、崩壊過程と同様に確率過程として扱います。それぞれのステージの人はそれぞれの平均速度vで動き回ります。速度分布はマックウエル分布です。カッコ内の数字が分岐比です。
図1
動き回る感染者は他人と接触します。接触する確率は、人口密度と断面積に比例します。人口密度は東京都の値です。断面積σ[m]が今回の計算での変更パラメータです。この濃厚接触者は感染率10%で感染し感染者となります。人口密度、接触の断面積と感染率の積が所謂感染確率ですが、ここではσだけを変えて様子を見ますので、以下ではσを感染確率と呼びます。
これらのプロセスを確率論的にモンテカルロ手法で記述し、何十万何百万の試行を繰返し平均を取ります。モデル空間は半径20㎞の平面で、最初の感染者を中心に置きシミュレーションを開始します。
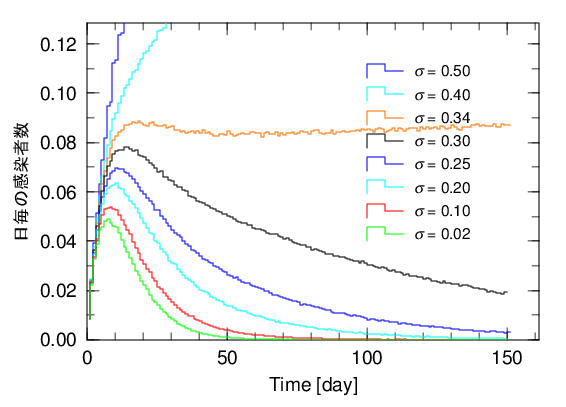
図2は、このようなシミュレーションを300回行った時の感染者の軌跡の例です。図3は、一人の感染者から感染した日毎の時間(日)変化です。感染確率σを変えた結果を示しています。σ=0.1の場合、一人の感染者から始まる感染はほぼ2か月で治まりますが、σ=0.3では感染が1年くらい治まりません。σが0.34以上では、感染は爆発的に広がり、一人の感染者から感染した人の数は膨大になります。
図2
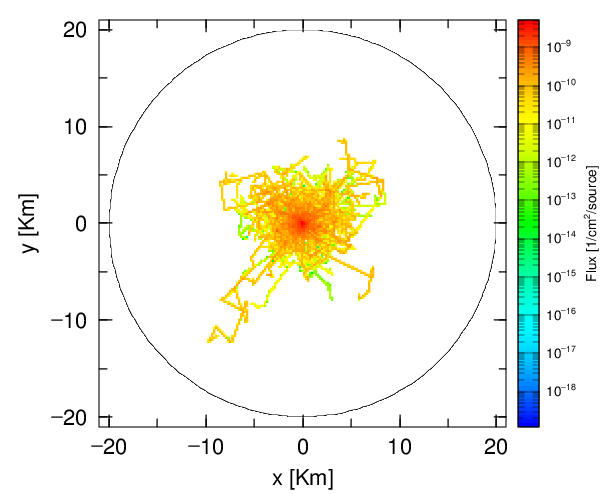
図3
このモデルを用いて、東京都の1月末から5月20日までの新規感染者数のデータと比較しました。初期の感染者は観測データをほぼ再現するように絶対値と時間分布を決めます。
具体的には図5のように2月9日から3月9日まで、3月20日から3月29日まで、3月30日から4月8日までの3期に分け、日毎強度をそれぞれ、0.1.3.0、5.0の比としました。総数は3902人です。
図6は、計算結果と東京都の日毎感染者数との比較です。新規感染者数の日毎変化(青、σ=0.1)は良くデータの形と総患者数5073人を再現します。同じ図に、4月7日の緊急事態宣言から、感染確率を80%減少した(σ=0.02)結果を黒線で示しています。患者数に変化がほとんど見られません。
さらに、5月12日から感染確率を3倍(σ=0.3)に増加させたときの結果を緑線で示しました。多少裾が上がりますが、急激な上昇は見られません。自粛をしない場合、感染者5078人、死者248人、自粛をした場合、感染者4975人、死者241人という結果です。
図5 初期感染者分布
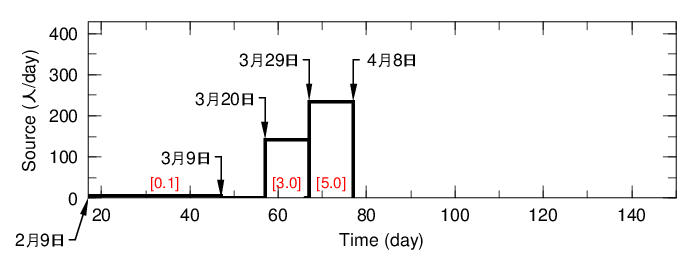
図6
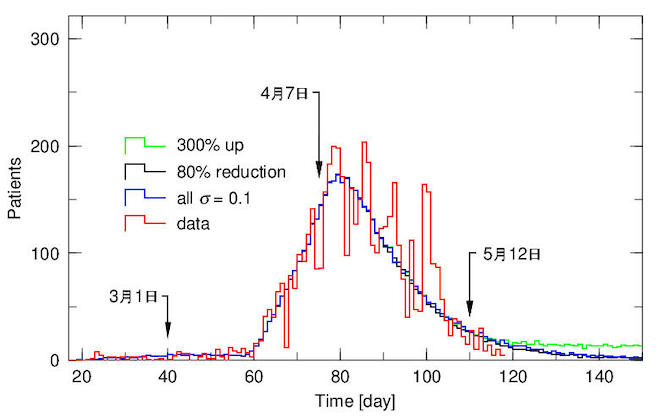
図7は、σ=0.34の結果です。このモデルでの感染爆発近傍の値です。データの上昇領域を再現するように初期感染者の総数を2600人に小さくしています。時間分布の形は同じです。ピーク以降はほぼ横ばいの値を示しています。図6と同様に、4月7日の緊急事態宣言から、感染確率を80%減少した(σ=0.068)結果を黒線で示しています。ほぼデータを再現しています。
また5月12日から感染確率を元の値(σ=0.34)に戻したときの結果を緑線で示しました。多少裾が上がりますが、急激な上昇は見られません。自粛をしない場合、感染者17381人、死者719人、自粛をした場合、感染者5058人、死者248人です。
図7
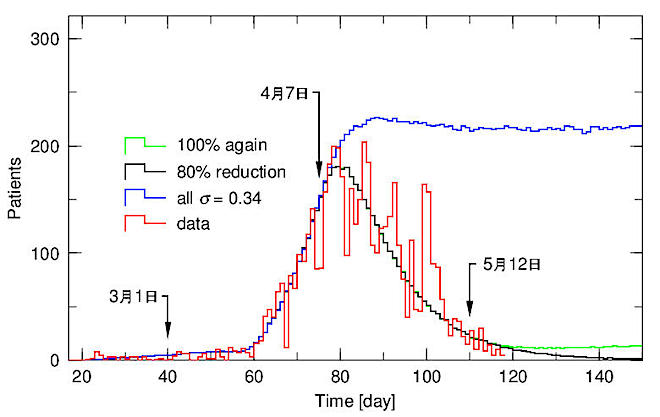
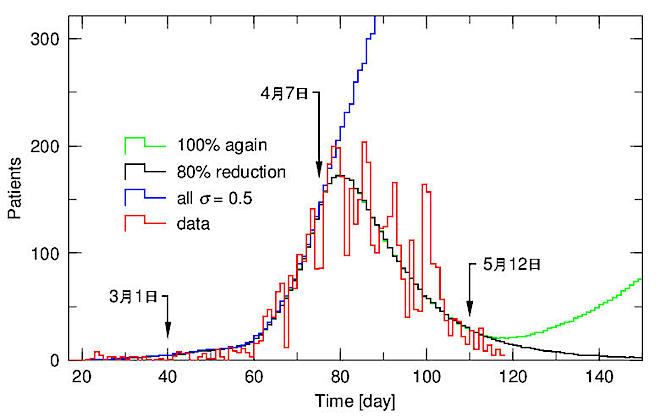
図8は、σ=0.5の結果です。初期感染者の総数を1500人に小さくしています。時間分布の形は同じです。図6と同様に、4月7日の緊急事態宣言から、感染確率を80%減少した(σ=0.1)結果を黒線で、5月12日から感染率を元の値(σ=0.5)に戻したときの結果を緑線で示しています。80%自粛した結果はデータを良く再現しています。
この図は西浦氏が示した、感染爆発が80%の接触低減で押さえられ、自粛を解除すると再び上昇するという図に似ています。このケースでは、自粛をしない場合、感染者100,060人、死者3098人、自粛をした場合、感染者5185人、死者251人です。
図8
簡単な感染拡散モデルを粒子輸送のモンテカルロコードPHITSに実装し、東京都の新規感染者日毎変化をシミュレートしました。フィットしたパラメータは、初期感染者の時間分布と強度です。このシミュレーションを用いて、感染確率σを変化させデータとの比較を行いました。
3つの感染確率σの場合の結果を示しましたが、緊急事態宣言の4月7日から感染確率σを80%減少させる所謂自粛を行うと、どの場合も東京都のデータを良く再現してしまいます。
つまり、感染確率σの値によっては、全くの自粛なしで大丈夫だったというシナリオも、西浦氏が主張した感染爆発の状態であったものが80%の自粛によって現状の状態に落着いたというシナリオも、両者とも成立します。従って、別種のデータから、この感染確率、SIRモデルでのR0の値を確定することが早急に求められます。これまでの措置の評価にも、今後の対応策にも非常に重要なものだと思います。