本書は長大な『21世紀の資本』を理解するための最小限の知識を解説したもので、すべての論点をカバーしていません。ピケティの本には膨大なデータが出ていますが、その説明は独特で標準的な経済理論とは違うので、経済学の知識がある読者にはかえってわかりにくいと思います。ここでは既存の成長理論との関連を解説しました。
資本主義の根本的矛盾
ピケティの結論は、最後の「結論」に要約されています。ピケティの主張は次の資本主義の根本的矛盾と呼ばれる不等式で表現されています。
r>g
ここでrは資本収益率、gは国民所得(GDP+海外収益)の実質成長率です。ピケティは「資本」という言葉を広い意味で使っているので、rは株式の場合は株主資本利益率(ROE)、土地などの固定資産の場合は賃貸料、金融資産の場合は金利で、その平均をとったものです。
ここで疑問なのは、rがつねにgより大きくなる必然性はどこにあるのかということです。この点を理論的に明らかにしたのが、ロバート・ソローの書いた長文の書評です。彼はピケティのいう資本主義の根本的矛盾がなぜ発生するのかを、彼のつくった新古典派成長理論で説明しています。
これを理解するには、成長理論を頭に入れる必要があります。ここではソローの新古典派成長理論をさらに省略した超簡単モデルを考えます。経済全体の生産量が資本と労働で決まると考え、この関係を生産関数と呼びます。労働人口を一定と考え、国民所得をYとし、資本ストックをKと書くと、生産関数は次のように簡単な形で書けます。
Y=F(K)
ここでYはKの増加関数ですが、その増加率はKが大きくなるにつれて下がっていく(資本は収穫逓減の法則に従う)と考えます。しかし資本は無限に増え続けるわけではありません。企業で減価償却として扱うように、一定の期間が来たら設備は古くなって価値がなくなります。
たとえば5年で償却して新しい設備に取り替えるとすると、資本の1/5は毎年なくなります。この消耗率をdとすると、毎年dKの資本ストックが失われるわけです。このようにマクロ経済的な均衡が実現して成長も止まるのが定常状態です(図1)。ここでsは貯蓄率で、投資は貯蓄sYと等しくなると考えます。
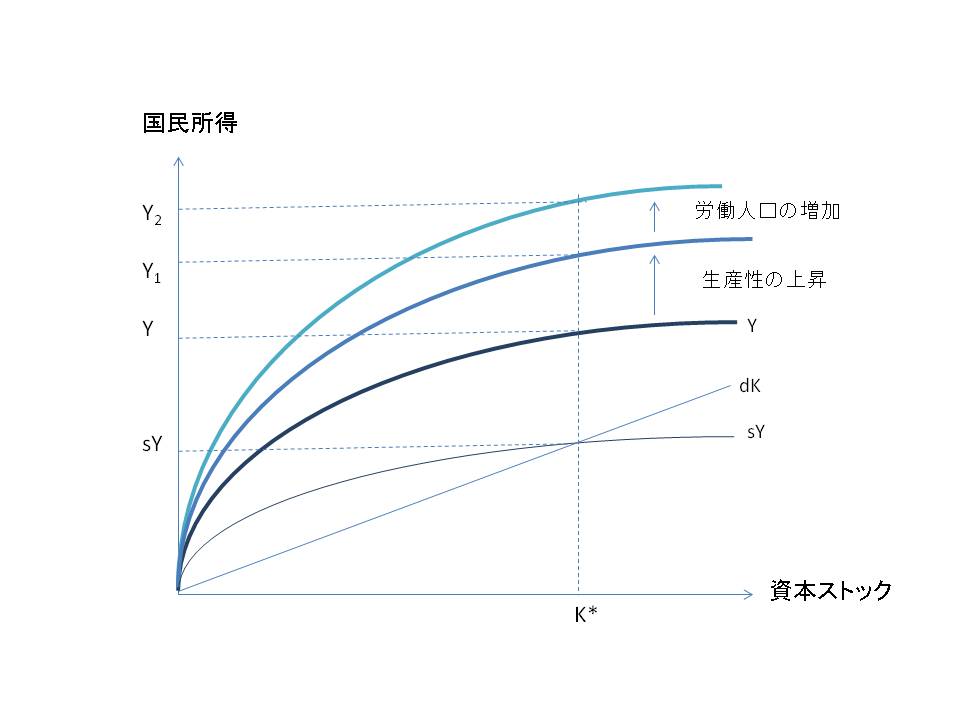
図1
だから毎年おこなわれるネットの資本蓄積はsY-dKで、これは図1のように資本ストックが増えるにつれてゼロに近づき、K*でゼロになります。この定常状態でsY=dKとなるので、それ以上、経済は成長しません。これがソローの新古典派成長理論です。ピケティの示しているデータは新古典派成長理論の定常状態と考えると理解できる、というのがソローの意見です。
経済が成長しないというのは奇妙にみえますが、技術進歩などで労働生産性が上がると成長します。これを成長理論では、生産関数が上にシフトすると考えます。F(K)には労働が含まれていないので、その関数そのものが変化するのです。この場合、労働者ひとりあたりの生産も増えるので、生産性に応じて賃金も上がります。他方、労働生産性が同じでも、労働人口が増えるとGDPが増えて成長します。ソローはこうのべています。
経済が資本/所得比率が一定の「定常状態」に到達したと考えよう。労働からだけ所得を得る人々の賃金は、技術進歩によって生産性が上がるのと同じぐらいのスピードで上がる。それは経済全体の成長率より少し低いだろう。なぜなら成長率は人口増加率を含むからだ。
つまり生産性が上がると、それぞれの労働者の所得は上がりますが、国民所得は労働生産性×労働人口で決まるので――人口が増えているときは――成長率は生産性の上昇率より高くなるのです。簡単にいうと、これが資本収益の上昇率が賃金上昇率を上回る原因です。
労働者は自分の生産性の上がった分しかもらえませんが、資本家は労働者を増やせば資本収益を上げることができます。図1に生産性の上昇を加えると、国民所得はY1のようになります。ここでそれぞれの生産要素の限界生産性に応じて所得分配が行なわれるとすると、資本家の得る利潤と労働者の得る賃金は、資本/労働比率に等しくなります。
しかし労働人口が増えてGDPがY2に上がったとすると、今度はGDPが増えたのは労働人口の増えた結果なので、賃金は変わりません(話を簡単にするためにK*は変わらないとします)。ピケティの「国民所得」は海外資産の収益も含んでいるので、海外の労働者を雇ったら資本収益は増えますが、国内の労働者に恩恵はありません。したがって限界生産性を超える収益(労働人口の増加や海外収益)は、すべて資本家のものになるわけです。
この結果、rがgを上回り、格差が拡大します。これをソローは富める者がますます富むダイナミックと呼びます。さらに資本収益が増えると資本蓄積が増え、それが相続されると格差はさらに拡大します。これがピケティのいう根本的矛盾r>gの理論的説明です。
格差は拡大するのか
このように短期的には、ピケティも批判するように、資本収益率は限界生産性では決まりません。しかし資本が蓄積されると、長期的には収穫逓減の法則でrが下がり、gと等しくなるのではないでしょうか。このとき資本分配率も下がり、格差は縮小します。これを打ち消す要因としては、生産性が上がってrが上がる可能性があります。
問題は、生産性上昇による不平等化と、収穫逓減による平等化の影響のどちらが大きいかです。ソローは歴史的には資本収益率は安定しており、この二つの影響はほぼ相殺されているといっていますが、ピケティは成長率が低下する一方で資本収益率は上がり、格差が拡大すると予想しています。そういうメカニズムは考えられるでしょうか。
これを考えるには、ソローの理論はあまり役に立ちません。それは「新古典派」という名がついていますが、実際には新古典派的に個人の合理的行動として資本蓄積を説明していないからです。ソローはケインズと同じく投資は貯蓄と等しくなるまで続くと仮定し、それが効率的かどうかは問題にしていないのです(一般には効率的ではない)。
この点をピケティは、第16章で黄金律として論じています。それによると資本蓄積が効率的に行なわれるとr=gとなるので、「基本的矛盾」は成り立ちません。これを厳密に証明するのは大変ですが、簡単にいうと、こういうことです。
ソローモデルでは資本蓄積sYと資本減耗dKが等しくなるような資本量K*で定常状態になりますが、これは最適とは限らない。永遠の将来にわたる消費を最大化する「代表的家計」を考え、ネットの所得F(K)-dKを最大化する条件は高校の微分を使うと、
F'(K*)=d (1)
となるときで、このK*が黄金律の水準です。ここで成長率F'(K*)はgだからg=d。他方、資本収益Rがその限界生産性で決まるとすると、ネットの資本収益R(K)-dKを最大化するのは、同様に
R'(K*)=d (2)
となるときです。ここでR'(K*)はrだからr=dで、(1)とあわせるとr=gということになります。これが黄金律で、図で描くとdKの傾きがgと等しくなるときですが、これを満たす貯蓄率sが実現するとは限らない。ソローモデルではsを政府が調節することになっていますが、ラムゼー以来の最適成長理論では代表的家計が貯蓄率を調節してr=gにすることになっています(図2)。
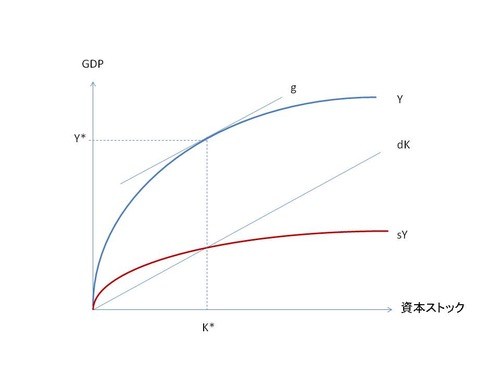
図2
ピケティは「もし黄金律が成り立つとすれば、rがgと一致するためにはβが10~15になる必要がある」といっています。黄金律の水準まで資本が蓄積されると、今は5程度のβがこれからまだまだ大きくなり、格差が拡大するというわけですが、この推定には疑問があります。もし最適なβが5に近ければ収穫逓減が起こり、rはgに近づきます。
このrは何をさしているのでしょうか。rを実質長期金利と考えると、一人あたり成長率gが1~1.5%であれば、日本では黄金律に近い状態が成立しています。rをROEと考えると、それは成長率に時間選好率(リスク・プレミアム)を加えたものですが、彼自身もいうようにこれはトートロジーです。時間選好率θは直接計測できないので、rとgの差として定義されるからです。
株式の収益率がr>gとなるのはリスク・プレミアムをθ=r-gと定義しているためであり、θがつねにプラスになる必然性はありません。θがゼロだと、やはりr=gになります。要するに資本収益率が成長率をつねに上回る必然性は、彼の理論ではうまく説明できないのです。
歴史的事実としても、これまでつねに資本収益率が成長率を上回ってきたわけではありません。1913年から世界の成長率は資本収益率(税引き後)を上回り、今も続いています。それは例外だとピケティはいいますが、100年も例外が続いたというのは無理があります。しかもこれは今後の資本収益率が成長率を上回るという予想で、現実には両者は交錯しています。
要するにピケティの理論は、資本の収穫逓減が起こらないのに成長率だけが下がるという奇妙な予想に依存しているのです。これは今までの100年間が戦争の続く例外的な時期だったからだと説明していますが、少なくとも今までの世界のデータでは、資本収益(課税前)は減少する傾向がみられます。それがふたたび上昇するかどうかは、彼がいうほど明らかではありません。
参考リンク
- Solow, “Thomas Piketty Is Right”
- Acemoglu & Robinson, “The Rise and Fall of General Laws of Capitalism”
- ピケティの公式ホームページ:Capital in the 21st century
- 講義ノート:Economics of inequality