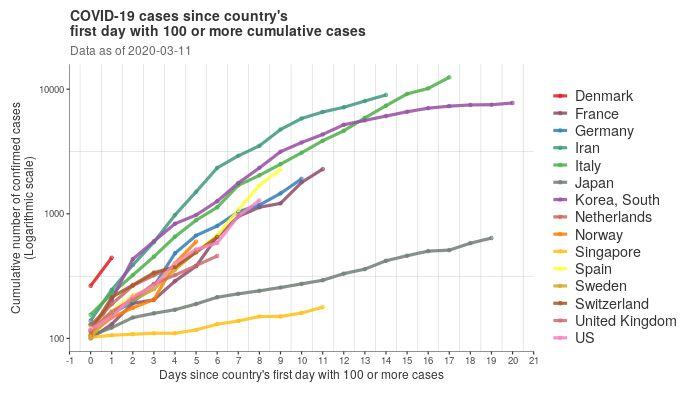
主な関係国について、新型コロナ感染者数の片対数グラフがある。
FT.comより
感染者数の伸びが日本は緩やかと解釈するのが普通だが、検査が少ないからとする解釈もある。本当はどうなのか計算してみる。
結論を先に書くと、検査が多いか少ないかは関係ない。
素朴な計算
感染拡大期には指数関数的に増える。グラフによると、日本・シンガポールを除く諸国では毎日約3割強増えている。t=0日でy=100人になるように式で表すとほぼ以下のようになる。(「10^3」は10の3乗を表す)
y = 100×10^(0.12t)
関数電卓でt=0、t=1、t=2くらいを計算してみれば、日毎に約1.3倍になる式だと確認できる。次に常用対数logをとり z=log y とすると、
z = log y = 2 + 0.12t
zはtの一次関数であり、t=0のときz=2となる。これが、上の片対数グラフにある、諸外国(シン以外)のグラフを近似した直線である。
さて、日本も諸外国(シン以外)と同レベルで感染者が増えていると仮定してみる。本当の感染者のうちrの発見率で見つかるとしよう。
y’ = 100×10^(0.12t)×r
この式は t=0 のとき y’=100 にならないので、あとで時間をずらす。先と同様に z’=log y’ とすると、
z’ = log y’ = 2 + 0.12t + log r
最後に t=0 のとき y’=100、すなわち z’=2 となるように時間をずらす。傾き0.12はそのままのため、次の式になる。
z’ = 2 + 0.12t
よく見ると z = 2 + 0.12t と全く同じになってしまった。つまり、日本も諸外国(シン以外)と同レベルと仮定すると、発見率rが小さいとしても、同じグラフになる。言い換えると、100人からのグラフは感染者の発見率には影響されない。
したがって仮定は誤りで、日本の本当の感染者数の伸びは緩やかということになる。
補足1
100人からの片対数グラフを最初に作った人は、以上のことを理解した上で作ったと思われる。関数処理に慣れていれば、グラフの意図にすぐ気づく。あるいはその分野の常識かもしれない。
補足2
上の素朴な計算では発見率rを一定とし、時間によって変化しないとした。もし時間とともにrが減少するなら結論が変わるはずと考えてみよう。
ところが、同じ仮定の下で計算してみればわかるが、rは指数関数的に急激に減少することになる。
r(t) ∝ 10^(-0.07t)
単純計算で10日間で1/5まで圧縮される。検査は次第に充実してきており、さすがにここまでのミスや不正を疑うのは無理があるだろう。
補足3
国内の感染者数の伸びが緩やかというのは過去の話。今後どうなるか私にはわからない。そういう議論は専門家に任せたい。
—
神 貞介 (じん ていすけ)京都大学 非常勤講師
東京大学大学院数理科学研究科博士課程を修了後、京都や大阪の大学で非常勤講師を勤める。