今回は自粛の効果検証の準備編で、統計的変動と依存的事象の区別についてです。用語が難しいですがお付き合いください。

nagi usano/Flickr
5月27日の緊急事態宣言の解除以降、テレビでは連日、新規感染者が、「〇人を下回ったのは〇日ぶり」「○人を上回ったのは〇日連続」と報道し、アゴラでおなじみの藤原かずえ氏に「NHKがこのような報道をしなかったのは24日ぶり」とつぶやかれるぐらいに、その数に一喜一憂しています。
本連載の③第2波は来るのかでも、緊急事態宣言解除以降の感染者数の増減から自粛は必要であったか、また、どのくらいの効果があったかを判断できると述べたので、毎日、新規感染者数を図に書き加えて眺めています。
図1は、6月7日までの全国の新規感染者数を加えた図です(以下の図は全て縦軸対数でプロットしています)。同じ図にモンテカルロシミュレーションを用いた3つの予測の線も示しています。黒線はこのモデルでの実効再生産数Rを0.41としてデータ全体をフィットしたものです。紫線は5月25日からこのRを0.77に増大させ、青線は1.37に増大させ、それぞれ自粛解除の影響を予測したものです。
今後、感染者のデータが黒線の上に乗ってくれば、自粛の効果はなかったことになります。紫や青線のように感染が再燃してくれば、自粛の効果が定量的に評価できます。これが、③第2波は来るのかの結論でした。
即ち、今後のデータとの比較で5月27日の自粛以降のRN値が決定できれば、自粛以前のR値もこのRN値と仮定すると、4月7日から自粛の効果でRNがRE =0.41になり、5月25日の自粛解除で再びRNに戻るというシナリオが成り立ちます。そうすると、4月7日以降を自粛なしのRNの値で全て計算した結果から、自粛をしなかった場合の感染者数と死者を出すことができます。その数こそが42万人といわれた予測を検証する数だと思います。
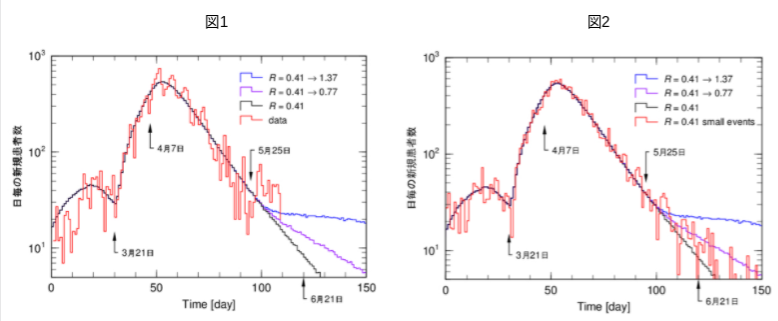
しかしながら問題があります。図1で5月25日以降のデータは、少し大きい値を続けていて青線に乗るような傾向にも見えます。また最近の新規感染者の数は全国で数十人の規模で、統計的変動が甚だ大きい状態です。今回は、この点について準備考察をします。今後、データが順次出てきたとき、それがどのように見えるか、モンテカルロシミュレーションを使って模擬します。
図1の黒、紫、青の結果は、モンテカルロ計算では、なるべく多くのイベント(事象、ヒストリーとも言います)を繰り返し、それらを平均して結果を得ています。図1の3本の線は10万回イベントの結果です。このスムーズな結果がモンテカルロ計算の求めるべき真値です。
逆に、意図的にイベント数を減らすと、統計的変動の大きな結果が得られます。
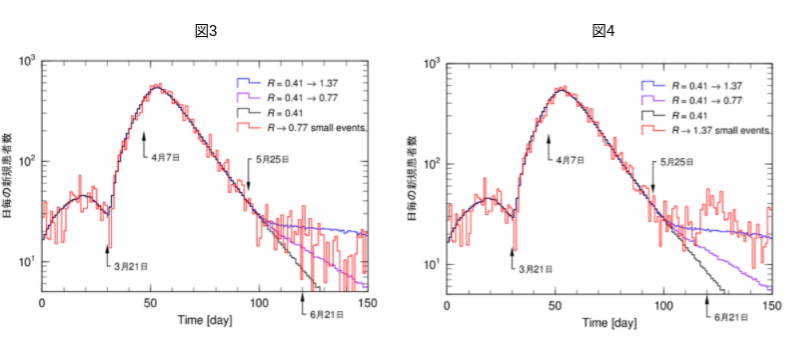
図2の赤線の結果は、黒線の条件で、7000回のイベントを計算したものです。実際の初期感染者数の規模のイベント数ですから統計的変動も実際のデータによく似てきます。このような操作をイベントジェネレータといい、モンテカルロ法を用いた仮想現実の作成です。測定器の評価や、統計処理の検証によく使います。
同じように、図3の赤線は紫線の条件で、図4の赤線は青線の条件で、同じく7000回のイベントの結果です。図4では、6月21日以降に山が見えますが、これは統計的変動の結果です。乱数の初期値を変えるとこの図とは異なる結果が生成され、そしてイベントを増やすと結果はスムーズな黒、紫、青線にそれぞれ収斂します。自粛の効果をRの変化として計算に取り込んだ(原因)の依存的事象が、この収斂した結果です。
一方、7000イベントで計算した赤線の結果は、原因(Rの変化)は同じように入っていますが、統計的変動がそれに上乗せになって見えている結果です。
これから実際の観測データが出てきますが、新規感染者数が少ない状況では、統計的変動が大きいため、自粛の効果を原因とする本来の依存的事象が統計的変動によって見えにくくなります。これがのデータの特質で、現在はまだ結論が出せる状況ではありません。
今回のイベントのシミュレーションの結果から、2週間後の6月21日ごろには自粛の効果を検証できる結論が出せるだろうと期待しています。
収束期の規制緩和の新しい指標としてK値が提案され、大阪府の吉村知事や神奈川県の黒岩知事が言及しています。K値の問題点については既に連載②K値は判定の指標になるか、でピーク周辺では真逆の指標となる危険性があることを指摘しましたが、収束期の領域では安定して使える指標なので、統計的変動を上手に排除してくれるのではないかと期待して使って見ました。
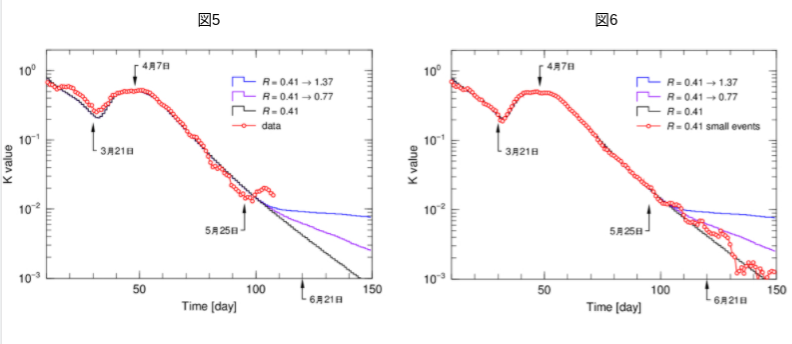
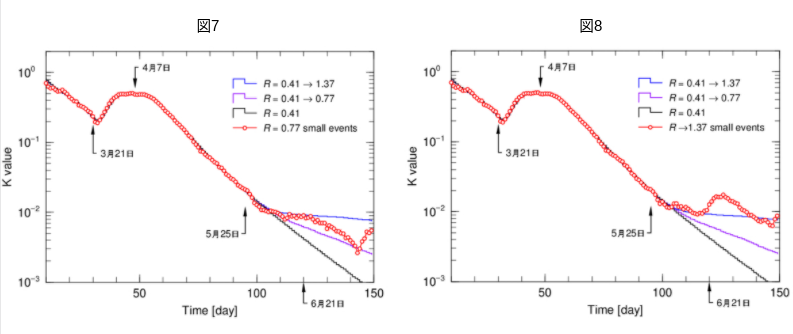
図5が図1の観測データと3本の計算結果から求めたK値です。図6、7、8は、それぞれ図2、3、4図に対応します。確かに統計的変動の小さい見易い図になっていますが、7000イベントで計算した各K値(図6、7、8の赤丸)がどの収斂した結果(黒、紫、青のスムーズな線)に乗るかは「一目瞭然」ではありません。
図5の5月25日以降の小さい山は、観測データですので、統計的変動なのか、特定の原因による依存的事象なのかは、実際の状況の解析がない限り分かりません。しかし、図6、7、8の赤丸の結果は、計算シミュレーションで生みだした仮想現実ですので、現れる山は統計的変動の結果であることが分っています。
K値は、手続きとして7日平均の操作が入るので、データの変動が平坦化され、統計的変動の強さが穏やかになります。しかし、この領域ではK値に直しても大きめの統計的変動が残り、依存的事象を明確にすることは難しいようです。やはりK値の提案者が言う通り、K値のもう少し大きい領域で、K値の変化から収束の傾向を予測し、それ以後の領域は予測線からのずれで統計的変動を判断するという使い方が無難なようです。
従って、今回のように、K値の傾向を予測した後の依存的事象の判定には残念ながら不向きでした。













