
nagi usano/flickr
これまでの記事はこちら。
図1
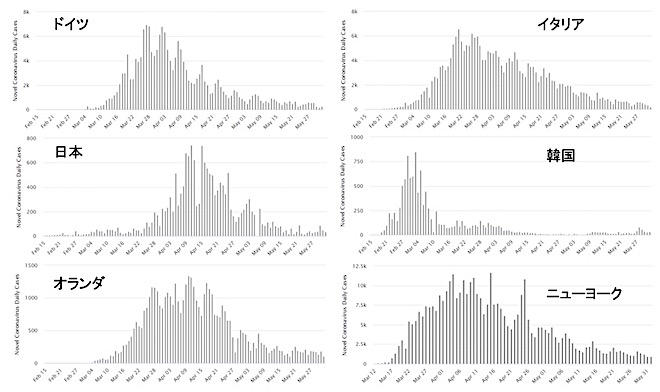
図1は、Worldometerのサイトから取った6か国の新規感染者数の日毎変化です。SIRモデルの教科書的解説では、感染が広がると罹患して免疫を持つ人が増え、その分罹患可能な人が減るので感染は治まる、とあり、この図の増減もそれに対応するとも言えます。しかし、今回のコロナは免疫保持者が少数で、このシナリオが成立するような状況ではないということも言われています。
一般の人はどう見るでしょうか。「各国とも急激な感染拡大に対してロックダウン等の防疫対策を行って何とか収束させた」と、また、「このまま何もしなければ、日本の死亡者数は最大42万人にも達する」という予測を聞き、「我々も我慢と忍耐を重ね、努力の結果感染爆発を食い止めた」と思っていることでしょう。
では、コロナはどうして治まったのか。このことを、完璧な感染防止策を取ったらどうなったのか、と逆から考えてみます。
日本で完璧に感染を防止できる透明軽量の「カンペキマスク」が発明されたとします。もちろん国民全員に配布してつけてもらいます。国内には新規発症者は既にいません。ただ、海外からの入国者に感染者がいることが懸念されます。そこで、入国者にも全員にこの「カンペキマスク」をつけてもらうことにします。
ある日、潜伏期の感染者1000人が一度に入国しました。もちろん「カンペキマスク」をつけてもらいます。これらの感染者は自覚症状がないので、入国後自由に行動します。さあ、どうなるでしょうか。
図2 図3
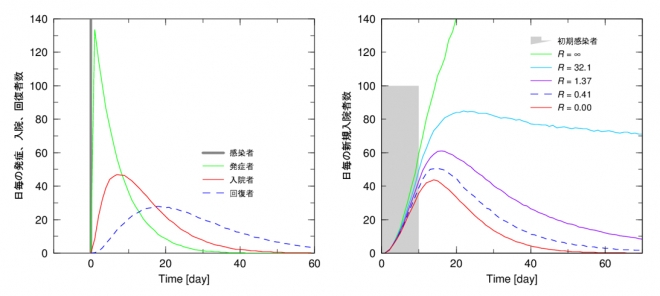
結果、新規入院者の日毎変化が図2の赤線です。図1の各国の感染者の推移の型はほぼこの赤線の分布の重ね合わせで記述できます。同じ図に発症者、回復者の時間変化も描いてあります。ここで用いているシミュレーションモデルでは、感染者は1週間で発症、更に1週間で入院、そこから2週間で回復または死亡というモデルを設定しています。
実際は個人差があり、平均値がこれらの日数となるような確率的事象として扱い、結果は図2のようなポアソン分布と呼ばれるものになります。この図2は、全く感染がなくとも、外部からの感染者の流入だけで、新規患者数の日毎変化は、感染が広がって、そして収束したというものですが、基本的に図1と同様の山形になることを示しています。つまり、感染者が4週間で治癒するということがコロナ収束の原理です。
さて、ここから感染の影響を入れます。図3が結果です。ここでは少し現実的に同じ1,000人の感染者の入国ですが、1日100人、10日間で入国したとします。グレー部分が初期感染者分布です。赤線が図2と同じ「カンペキマスク」着用の結果です。
このマスクを外し、感染が発生する状況をシミュレーションしますが、感染の強さを表すパラメータが必要です。再生産数Rを定義します。これは「実効再生産数Rt」に相当します。このモデルで感染に関するパラメータを決めたときに、ひとりの人から何人の人が罹患し入院したかという数を実際にシミュレートして得た値です。Rの増大に伴い、感染者が増えていきます。コロナ感染の収束は、治癒時間と感染速度の関係で決まります。感染速度が治癒時間より速いと感染拡大しますし、遅いと収束に向かいます。
以上を踏まえて、日本、中国、イタリア、ニューヨークについて、新規感染者の日毎分布を模擬してみました。図4から図7です。データはウィキペディアから取っています。この解析では、まず、初期感染者の分布とその絶対値を最初のピークを再現するように決め、次に、収束期のテールの振舞を合わせるようにRを決める。という方針でデータをフィッティングしています。
武漢、イタリアやアメリカの病院、また、日本の3月の帰国者などの様子を見ると、感染初期に局所的にRの大きい感染が発生し多くの感染者を生んだと考えられます。この初期部分はシミュレートせず、その結果を初期分布の情報に組み込んでいると仮定し、その後の穏やかなRによる社会での拡散をシミュレートするという方針です。
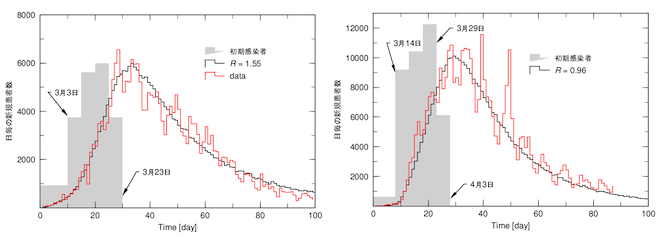
以下の図には初期感染者の分布、Rの値が示してあります。Rの値は日本と中国が1よりだいぶ小さく、イタリアが1.55とニューヨークが0.96です。いずれの場合も、初期に大きい感染者数を設定すると、その後2か月の変化を実によく再現することができます。フィットで得られた初期分布も、それなりに現実の事象に対応しているようにも見えます。
例えば、日本は2つの初期分布を与えていますが、3月10日までのものは、武漢からの入国が起源、3月21日からのものは、ヨーロッパからの帰国者起源とみることができます。中国のデータの収束過程をフィットしようとすると、ほとんど感染がないR=0.01と小さい値を取らないと合わせられません。
この結果はR=0の結果とほぼ同じです。中国は早めのロックダウン解除や、通常生活への復帰があり驚きましたが、このデータは確かに中国社会のもつ感染力Rが非常に小さいことを示しています。
図4 日本 図5 中国
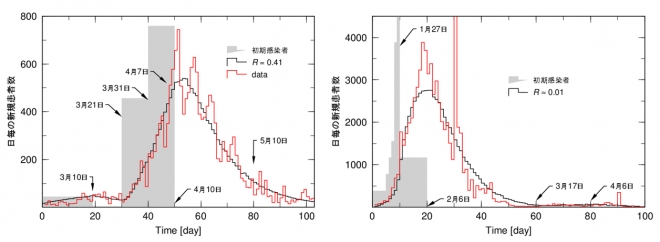
図6 イタリア 図7 ニューヨーク
結論:幾つかの事象をシミュレーションで再現できても、含まれる仮定や物理モデルが正しいということの証にはなりません。まして、今後の全ての事象を正しく予言できるわけではありません。しかしながら、これまでのデータを再現できないシミュレーションに、今後のことを託すわけにはいきません。
「ヒトとの接触8割削減をしないと42万人死亡」という予測が現実と大きく異なった今、モデルのパラメータを設定しなおして、上で示したような、これまでの観測データを再現する図を示さなければなりません。パラメータ設定で再現できないなら、使っているモデル自体がこの事象解析には不適切ということになってしまいます。
追記:テレワーク在宅勤務中で、結局自分で計算してしまいました。関係者から「面白い記事を読みました」とメールを頂きますが、最近、末尾に遠慮がちに、「あの案件はどうなったでしょうか」というのをちらほら見かけるようになったので職場復帰します。幸い、大学の方からこのPHITSコードを使いたいという申し出を頂いたので、今後このPHITSが研究の手助けになれば幸甚です。














