前回の論考の最後のところで、米CDCによるコロナワクチン副反応解析の隠蔽疑惑について少し言及しました。今回はこの疑惑について詳しく説明してみます。

米CDC アトランタ本部 Wikipediaより
コロナワクチンと心筋炎との関連性はJAMAの論文において示されました。この論文では米VSDのデータを用いて解析しています。VSDはCDCによるワクチン安全性監視システムです。
この論文では、23種類の有害事象について、接種後1~21日のリスク期間の発生率と接種後22~42日の比較期間のそれを比較しています。そして、調べたすべての有害事象において前者の発生率が後者のそれより有意に高くなかったことが示されました。つまり、心筋炎を含むすべての有害事象においてワクチンとの関連性は示されなかったということです。
心筋炎だけは特別な補足解析が実施されました。 具体的には、年齢を12~39歳に限定し、リスク期間を接種後0~7日に変更して同様の解析が 実施されたのです。その結果、ワクチンと心筋炎との関連性が示されました。
問題は、論文内で脳梗塞、心筋梗塞などの他の有害事象において同様の補足解析を実施したかどうか について記載がない点です。実施したのであれば、その結果について記載するべきです。実施した結果、他の有害事象では有意差がなかったのであれば納得できます。実施していないのであれば、未実施の理由を記載するべきです。
高齢者に限定し、リスク期間を接種後0~7日として、脳梗塞や心筋梗塞のデータを補足解析すれば、 有意差が認められる可能性があると、私は考えています。つまり、CDCの隠蔽疑惑というのは、心筋炎以外の有害事象の補足解析の結果を、CDCは意図的に公表していないのではないかという疑惑なのです。
脳梗塞や心筋梗塞の補足解析で有意差がでた可能性は、日本のデータより示唆されます。厚労省が公開しているデータを集計し、接種から発症までの日数と報告数のグラフを作成しました。重複例は削除してあります。
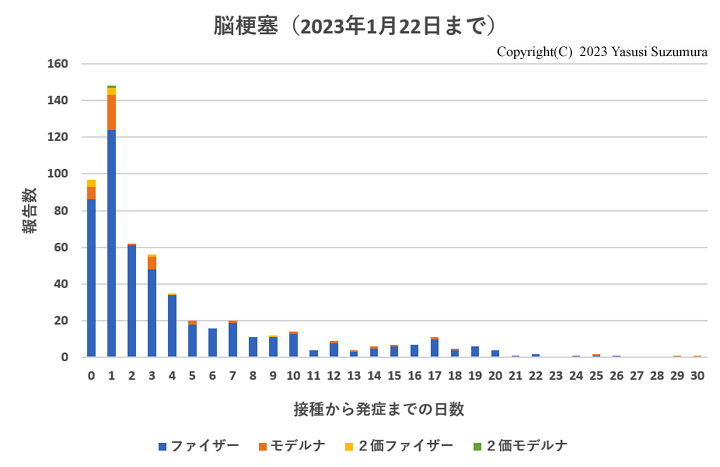
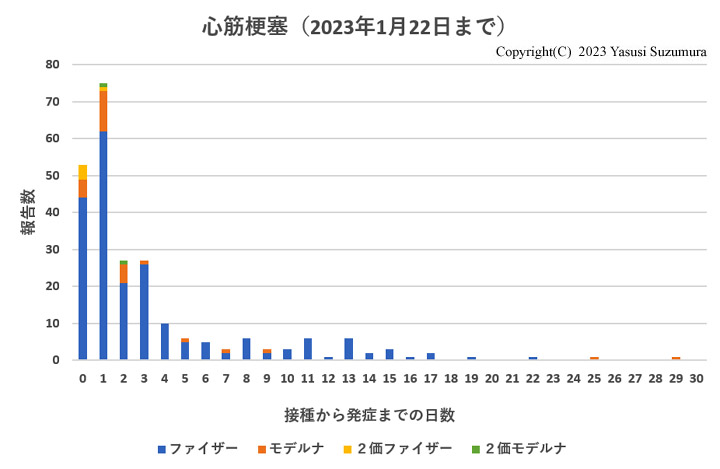
脳梗塞と心筋梗塞の発症は、ワクチン接種後7日以内に集中しています。したがって、リスク期間を接種後0~7日に設定すれば、有意差が認められる可能性は十分にあります。ただし、報告バイアスの問題があるため立証できたとは言えません。立証のためには、米VSDのような極力バイアスを排除してデータ収集できるシステムが必要です。
CDCの隠蔽疑惑については、以前に発表した論文においても指摘しました。ASA声明 では、「科学的推定のためには実施されたすべての統計解析の結果が公表されるべき」としています。何らかの意図を持って選択された解析結果のみが公表されると、 適正な科学的推定とは言えなくなってしまうのです。
【佐藤正さんへの反論】
私はFacebookには参加していませんので、こちらに反論を書いておきます。
今回の私の論考はSCRIデザインによる統計解析の話です。佐藤さんが反論のために提示した論文は2編ともSCCS法による統計解析による論文です。SCRIデザインによる統計解析の話をしている時に、別の統計手法の論文を提示して反論することは、あまり論理的とは言えません。
SCRIデザインによる心筋梗塞などでリスク期間を接種後0-7日に設定して解析した論文は発表されていないはずです。
SCRIデザインはSCCS法に似ている部分もありますが大きく異なる部分があります。SCRIデザインは接種者のみを対象としているのに対して、SCCS法では接種者と未接種者を対象としています。私が再三主張している「偶発性の検証」という点ではSCRIデザインの方が優れています。同じデータを用いても、統計手法を変更して解析すると、結論が逆になってしまうことは有り得ます。
データ収集後に評価方法を変更することは本来望ましくありませんが、接種後どの期間に発生が多くなるかはデータ収集した後に判明することなので、SCRIデザインの場合、データ収集後にリスク期間を変更追加して解析することは仕方のないことと考えます。むしろ、最初に決めた不適切なリスク期間のまま解析してしまうことの方が問題です。
【佐藤正さんへの反論2】
(1)「Hippisley-Cox et al. BMJ, 2021」の論文
https://www.bmj.com/content/374/bmj.n1931
Period event incidence rate ratio (95% CI)
01-07 days 1483 0.90 (0.85 to 0.95)
08-14 days 1668 0.98 (0.93 to 1.03)
…….以下略
このデータは、この論文内のFig1で示されたmyocardial infarctionのデータと思われます。確かにこのFig1では、Incidence rate ratioは「1-7の期間」が他の期間と比べて
高いわけではありません。
問題は、このIncidence rate ratioの計算方法です。
Methods Study design and periodには次のように書いてあります。
ケースシリーズでは、対象となる転帰を持つ人々において、曝露した期間(例えば、ワクチン接種やSARS-CoV-2感染後)と曝露していないベースライン期間とを比較して、対象となる転帰の相対発生率を求める(see supplementary fig 1)。
つまり、SCCS法によるIncidence rate ratioであって、SCRIデザインによるIncidence rate ratioとは異なる数値なのです。SCCS法は、曝露していないベースライン期間とか未接種者のデータを含めた解析方法であるため、SCCS法によるIncidence rate ratioでは偶発性を検証したことにはなりません。
(2)私は何も断定はしておりません。
「報告バイアスの問題があるため立証できたとは言えません。」と書いています。SCRIデザインによる解析が不十分なことに対して疑問を呈しているだけです。
【佐藤正さんへの反論3】
反論2はやや雑でしたので、今回はもう少し細かく書きました。
(1)どのようなデータが提示されれば私が納得するか
a.報告バイアスが極力排除されて、データが収集されていること
b.接種後日数のグラフ(私が提示したようなグラフ)が提示されること
c.リスク期間を適切に設定してSCRIデザインで解析すること
d.接種回数、年齢層を限定した解析も行うこと(心筋炎の解析ではこれが実施されている)
bのグラフ作成は特に重要です。グラフを見れば偶発的な発症かどうかが明白になります。 公表された論文で、このようなグラフを見た記憶がありません。 また、グラフにおいて接種後0~2日に発症が集中していれば、リスク期間を0~2日にする必要があります。 つまり、0~7日の期間の間でも発生に偏りがある可能性も考慮する必要があるわけです。 それをはっきりさせるにはグラフの提示が必要です。
また、dも重要です。心筋炎の解析の時のように、接種回数、年齢層を限定した解析を実施すると結論が変化する可能性は否定できません。
(2)コホート研究、SCCS法で有意差が認められない理由
ワクチンによる心筋梗塞の発生率は、それほど高いわけではなく、そのため有意水準5%では 有意差が認められないのだと推測されます(第2種の過誤の疑い)。 つまり、コホート研究、SCCS法で因果関係を完全に否定するのは無理という話です。 この場合、立証できる可能性はSCRIデザインによる偶発性の検証であり、そのためには、 まずグラフを作成してみる必要があります。
(3)接種後数日以内にアナフィラキシー以外に何らかの重大な異常が生じている可能性
α評価認定例は「何らかの心肺の障害が生じた可能性が推定された」1件のみですが、この症例 は接種数分後より発症しています。当初アナフィラキシーが疑われていましたが、現在はその可能性は低いとされています。 広島大学が、2回目の接種後1~10日で死亡した20~50代の男性4人の 解剖例を論文で報告 しています。 血液サンプルを「RNAシーケーシング」により分析し、サイトカインの過剰な放出が死因であった 可能性を推測しています。 つまり、接種後数日以内は、アナフィラキシー以外の致死的な有害事象が発生する可能性があるわけです。
サイトカインの過剰な放出では血圧が急上昇する可能性があり、それに伴い心筋梗塞、脳出血などが 誘発される危険があります。実際に 接種直後の血圧上昇の報告 は非常に多くあります。
ただし、その発生率はさほど高くはないため、コホート研究とSCCS法では有意差が認められない と言うことです。 そのため、心筋梗塞、脳出血、脳梗塞、接種後死亡などの接種後日数のグラフを作成しSCRI解析をして、 偶発的な発症と言えるのかを確認する必要があります。 それらが論文として公表されない限り、私の疑念が晴れることはありません。 現在の統計解析には再考の余地が残されているというのが私の主張です。
【佐藤正さんへの反論4】
(1)「接種回数、年齢層を限定したSCRI解析も行うこと」に意味はあるか?
あまり意味がないと思う人がいるかもしれませんが、これは重要な意味があります。 その根拠を示します。
厚労省が公表している「接種後死亡者一覧」のデータをVBAを用いて集計しました。 非死亡者を含む「疑い例一覧」の方が望ましいのですが、接種回数の欄は「疑い例一覧」の方には何故か存在 していないため「死亡例一覧」の方を使用します。 報告バイアスのあるデータですが、1回目と2回目には同様のバイアスがかかっていますので、 1回目と2回目を比較することは意味があります。
心筋梗塞で死亡、接種1回目の人数は58人、2回目は48人でした。1回目は2回目の1.21倍でした。 これを65歳以上で集計すると、接種1回目の人数は49人、2回目は32人でした。1回目は2回目の1.53倍でした。したがって、接種1回目、65歳以上、リスク期間0~2日でSCRI解析すれば、有意差がでる 蓋然性は高くなるはずです。
なお、1回目の死亡が多くなる傾向は、脳出血、脳梗塞でも認められます。 脳出血で死亡、接種1回目の人数は32人、2回目は17人でした。1回目は2回目の1.88倍でした。 したがって、他の疾患でも、接種回数、年齢層を限定したSCRI解析が必要です。
また、脳出血による死亡が偶発的な死亡だと考えた場合、何故1回目と2回目で死亡数が大きく異なる のかが説明できません。偶発的死亡であるならば同じ程度の死亡数になるはずです。
(2)私が細かいことに非常にこだわっている理由
帰無仮説を「コロナワクチンと心筋梗塞との関連性はない」とした場合、 p値が0.05未満の時に帰無仮説は棄却され「関連性はある」という結論になります。 一方、p値が0.05以上の時は、帰無仮説は棄却も肯定もされません。 発生率が低いためにp値が0.05以上となることがあるためです。したがって、 「関連性は不明」という結論になるわけで、「関連性がない」という結論にはなりません。 厳密に言いますと「有意差がなかった」は「関連性がなかった」を意味しているわけではありません。
何が言いたいかと言いますと、「関連性を否定すること」は、「関連性を肯定すること」 より、遥かにハードルが高いということです。 ASA声明でも、科学的推論を行う時には、複数の方法で解析するべきとしています。 つまり、関連性を否定する場合には、あらゆる観点より、微に入り細に入り検討する 必要があるということです。それらをクリアーして初めて関連性が否定されることになります。
(3)後から評価方法を変更することは、絶対だめなのか?
グラフを作成した後に、グラフより判断して適切なリスク期間を設定することに問題があるとは思えません。 グラフを作成後でなければ、適切なリスク期間かどうかを判断できないからです。 また、ある研究グループが有意差が認められる条件を見つけて公表した場合、別の国の研究グループが別のデータで、公表されたその条件で解析して有意差が確認できれば、後付けの評価ではなくなります。 つまり、最初の研究成果が次の研究につながったわけです。
また、心筋炎では追加の解析が認められるが、心筋梗塞や脳出血では追加の解析が認められないというのは、おかしな話です。
(4)コホート研究で有意差が認められなくても、偶発性の検証で有意差が認められる可能性がある。
この主張は、 私が1年くらい前より繰り返し発表している主張 です。 佐藤さんの影響で、考えが変わったわけではありません。 繰り返しになりますが、世界で標準で実施されている解析では不十分であり、 解析方法には再考の余地があるという話です。
私も、今回の反論で、いったん議論を終了とします。
議論に付き合っていただき、ありがとうございました。
【佐藤正さんへの反論5】
統計を誤解していると言われてしまったので、もう少し議論を続けます。
(A)統計の誤解とは、(2)のことか、(3)のことか、あるいは両方か、その点は、はっきりさせてください。
(B)(2)に関して言えば、間違っているとは、私は思いません。
「有意差なし」を「関連性なし」と解釈してはいけないということは、 以前にNatureで指摘 された有名な話です。多くの研究者が誤解しています。
ポイント部分を引用しておきます。
「統計的有意差がある=薬効がある」なら「統計的有意差がない=薬効がない」と考えてしまいそうだが、声明ではこのように有意差がない場合、「“差がない”あるいは“関係がない”といった結論をしてはいけない」としている。
(C)(3)に関しては、様々な反論があることは理解できます。
【佐藤正さんへの反論6】
(1)佐藤さんのコメントが変更されていました。誤解とは(3)についてのようです。
言わんとすることは理解できます。私の書き方には問題がありました。
次のような主張にします。
疑い例の報告データより、心筋梗塞が接種後1週間以内、特に2日以内に集中して発症している ことが疑われる。 そのため、報告バイアスが極力少なくなるようにデータを収集してSCRI解析する研究を企画する。 接種1回目と接種2回目は発症率が異なる疑いがあるのでそれぞれ解析する、 年齢は65歳以上と65歳未満に分けて解析する、リスク期間は接種後0-2日、3-7日、8-15日 として解析する。
上記のような研究を今後日本で実施するべきである。
(2)CDCが論文作成時に事前に把握していた可能性のある事実
当時アメリカにおいても接種後死亡が接種後1週間以内に集中しているグラフをCDCが公表していました。 1週間以内の死亡には心筋梗塞や脳出血が多数含まれていました。 つまり、接種後1週間以内に心筋梗塞や脳出血が集中して発症しているかどうかは当時問題となっていたはずです。 その疑問を払拭させるには、リスク期間を0-7日にした補足解析が非常に有用であったはずなのです。 そのような事前情報があったのにも拘わらず、心筋梗塞などの補足解析を実施しなかったことには疑問が残ります。
【佐藤正さんへの反論7】
佐藤さんのコメント
何かいい例がないかと思うのですが、この話はさいころ2回ふって、4が連続でたから、4が出やすいさいころだという仮説を設定して統計検定しよう、4が連続で偶然で出る確率は1/6×1/6だからp<0.05だね。よしこれは有意差だ!サイコロ使ったいかさまは重大な問題だから厳しい統計の基準を使う必要がある!有意差がないと不正がない事は違う!とかいっているのとと概念的には基本的に全く同じなんです。
これは、反論4の(2)及び反論5の(B)に対するコメントと思われますので、反論しておきます。
「有意差なし」を「関連性なし」と解釈してはいけないと言う主張は、私の主張ではなくて、 科学者800人超の署名入りでNatureで発表された声明 においての主張なのです。
重要なことなので、もう一度引用しておきます。
「統計的有意差がある=薬効がある」なら「統計的有意差がない=薬効がない」と考えてしまいそうだが、声明ではこのように有意差がない場合、「“差がない”あるいは“関係がない”といった結論をしてはいけない」としている。
一流の800人超の科学者による主張を否定するわけですから、もっと論理的で明快な説明をしてください。 そして、Natureで発表された800人超の科学者の声明は、このような理由で間違っているとの論考を Natureにぜひ投稿してください。期待しています。













