タレブがウェブサイトに出した”Antifragile”の数学付録がちょっとおもしろいので、紹介しておこう。ここで彼は、投資銀行や経済学者がなぜ「ブラック・スワン」を見落とすかを説明している(テクニカル)。
経済学の理論でもっとも疑問の余地のない理論と考えられている比較優位を考えてみよう。たとえばポルトガルの衣服のコストがイギリスの90%であるのに対して、ワインのコストが50%だとすると、ポルトガルは衣服をつくるのをやめてワインに完全特化し、その代金でイギリスから衣服を輸入することによって利益を得られる。イギリスも衣服に特化して同様の利益を得ることができる。
しかしある年、葡萄が大凶作になって、ワインの生産量が20%ぐらいに落ちたとしよう。そうするとワインの生産に完全特化たモノカルチャーでは、人々の大部分が職を失う。つまりワインのコストは定数のようにみえるが、こういうリスクを含んだ関数なのだ。
ところが経済学では、コストや生産量を与えられたパラメータとして、その関数を考える。資産選択の理論の古典となったマーコウィッツの論文では期待値と分散が正規分布に従うと仮定してリスクを計算しているが、彼は論文の最後に「市場で観察される期待値や分散は誤差を含む」と書いている。実際には、分散や共分散は測定方法で大きく違い、変動も大きいことが知られている。
たとえば2005年に全米の住宅価格の変化の共分散がゼロだったとすると、サブプライムローンの設計者はなるべく多くの地域の住宅価格を組み込んで証券化すれば、個々のリスクは大きくても全体として相殺されると考えた。しかし2007年以降、住宅価格そのものが確率変数であることに多くの人が気づくと、ニューヨークとLAの住宅価格が同時に暴落し、共分散は1に近づく。

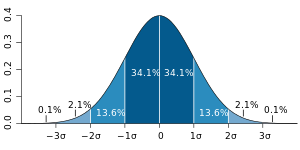
上の図のようにランダムな正規分布の場合は3σ以上のテールリスクが発生する確率は1/740だが、標準偏差に誤差が含まれていると、それが5%上がっただけで3σの発生確率は60%も上がる。人々がテールリスクを見逃す一つの原因は、このように誤差を含む確率変数を定数と思い込み、それをもとにした関数でリスクを計算することにある。すべてのリスクは、こうした誤差についてのメタ確率をもとにして計算すべきなのだ。
確率変数を定数と考えて失敗した不幸な例が、福島第一原発事故である。東電はあらゆる事故原因を想定した上で、それに対する対策を実施していたが、そこで使ったパラメータが致命的な誤差を含んでいた。マグニチュード8以上の巨大地震が福島沖で起こる確率は、国の基準では0.0とされていたが、これが間違いだったのだ。
原論文は簡単に数学的な説明もしているが、彼は今このコンセプトをくわしく展開した教科書を書いているようだ。このドラフトもGoogle documentで読める。