
Mikhail Dmitriev/iStock
(モンテカルロシミュレーションで検証 連載50)
山火事理論の定式化は、自己無撞着な取扱い、燃焼率の一般化と半値幅の普遍性が言えたことで、論文としてまとめました。興味ある方は、このリンクにプレプリントをアップしましたのでご覧ください。これまで経験のない研究分野での初めての論文で、まだ査読前です。ご留意ください。
本稿では、この山火事理論を用いてオミクロン感染拡大におけるブースター接種の効果を検証しました。結論は、感染者総数で52%減(827万人減)、死亡者総数で28%減(4800人減)という抑制効果があったというものです。
1.山火事理論とは
永江一石氏、中村幸嗣氏の提案した山火事理論は、「感染爆発が起きると、燃えやすいところが燃え尽きることで周りに弱いながら自然感染免疫ができて収束する」という仮説です。
まず、感染症の数理モデルの基礎と言われるSIRモデルについて簡単に述べます。変数は、未感染者(S)、感染者(I)、回復者(R)です。未感染者は感染者と接触して感染し、感染者は一定期間で回復し、回復者は免疫を得て再度感染しません。従って、感染拡大と共に未感染者が減少し、未感染者がある割合以下になると、感染が収束するという集団免疫のメカニズムを記述しています。
SIRモデルの問題点は、未感染者の初期値として、国民全体を仮定することです。例えば、昨年の日本のデルタ株の感染者の総数が92万人で、これは人口のわずか0.7%です。この比率では、集団免疫というシナリオはまったく機能しません。
しかし、専門家が理由が分からないと言うなかで、急激に収束しました。この問題はコロナの当初から世界で論じられ、国民全体を均一な感受性を持つ者と仮定するのが問題で、感受性を持つ者(未感染者)の不均一性を導入する必要がある等、いろいろな改善の方策が提案されました。しかしながら、不均一性を定量的に評価しモデルに組み込むことは、あまりにも曖昧さが大きく現実的ではありません。
山火事理論の提起した発想の転換の核心は、感受性保持者の人数を初期値として設定するのは不適当である、ということです。そこで導入したのが、
燃焼率κ = 感染者総数 / 感受性保持者総数
です。
燃焼率κを初期値として指定すれば、感受性保持者総数は従属変数になります。そのためには感染者総数を知る必要がありますが、これはこの方程式の解そのものです。このように、方程式の変数に方程式の解そのものが含まれる方程式を自己無撞着(self-consistent)な方程式と呼びます。数値解法として、逐次代入法を用います。即ち、試行解を用いて次の解を求め、更にその解を用いて次の解を求め、解が収束するまで続けます。
この自己無撞着 (self-consistent) な方程式では、燃焼率κ を与えることによって、感受性保持者総数を初期条件として設定せずに、感染者総数を求めることができます。ここでκ = 1 即ち、「燃えやすいところが燃え尽きる」のがこれまでの山火事理論ですが、このκ = 1 という条件は、ひとつの大きな仮説です。
そこで、κ の値を一般化して(0<κ≦1)、自己無撞着な解を検討すると、ピークの半値幅(FWHM:半値全幅)がκの値によってユニークに決まることが分りました。また、現在検証している15カ国の過去のピークと比較すると、κ = 1の条件で全てのピークの半値幅が再現されることが分りました。即ち、κ = 1、これを完全燃焼条件と呼びますが、これは、初期条件として設定した仮説ではなく、コロナの感染拡大、収束のメカニズムの固有の性質であることが示されたわけです。
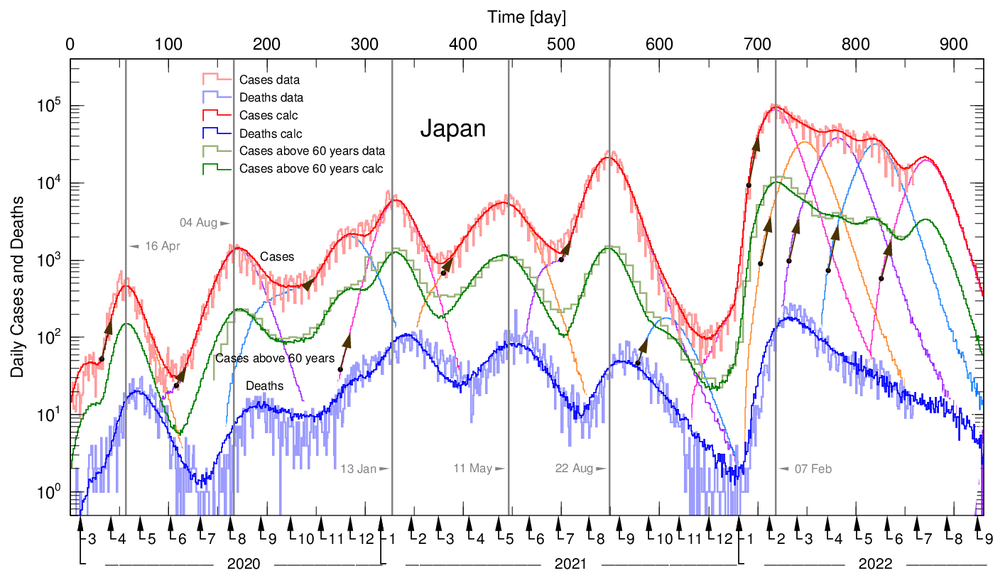
図1
図1は、日本のこの2年半の陽性者数、60歳以上の陽性者数、死亡者の変化と、これを変異株毎、また連続的な変異のところも幾つかの波に分解して山火事理論を適用した結果です。
各波について、感染確率(基本再生産数R0で特徴付けられる)の値は図1に示す矢印の基点で決定しています。基点の後、感染確率は時間変化せず、ピークの位置と高さは自己無撞着な解によって自動的に決定されます。全ての波の半値幅は、κ=1.0の条件で再現することができました。
2.ブースター接種の効果を定量的に評価する
山火事理論の特長のひとつは、ワクチン接種、人流制限等の対策効果を定量的に評価できるところです。何故なら、感染対策とは別個に独立した感染拡大収束の独自のメカニズムを理論に内包しているからです。
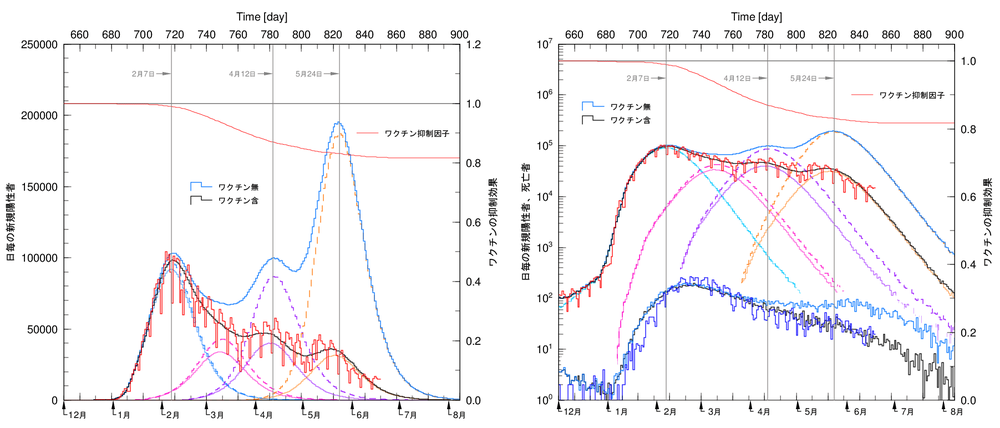
図2
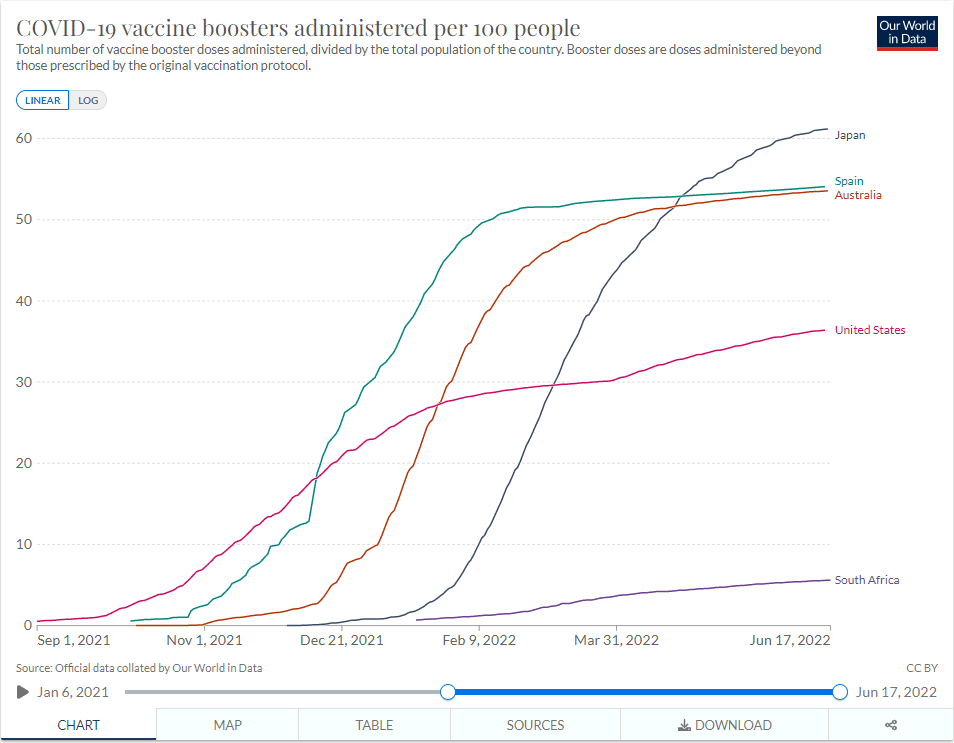
図3
山火事理論でワクチン接種の効果を評価する場合、普通に考えればワクチンによる感染抑止効果の時間変化を定量的に外部から与える必要がありますが、もし、ひとつのピーク期間にワクチンの抑止効果が時間的に一定であれば、その効果は初期値R0に既に含まれるはずですから、外部から与える必要がなくなります。
評価対象は2022年1月から6月中旬までのオミクロン株の感染拡大です。現在6月中旬以降、感染者数は再び徐々に上昇に転じ、ワクチン効果の減衰と言われていますので、評価はそれ以前の期間にします。この期間、日本ではちょうど3回目のブースター接種が進み、6月中旬には接種率が約61%に達しています(図3)。
アドバイザリーボードで報告されている感染抑制効果から、ワクチンの種類、年齢層にもよりますが、2回のみの接種の発症予防の有効性は約30%、3回接種の有効性を約60%とすると、ブースター接種による有効性の上昇は30%となります。抑止効果は接種から2週間で発現、経過時間による有効性の減衰はないと仮定すると、ブースター接種の抑止因子は、2回接種の有効性を基準として、平均で最大で30%×61%=18.3%、時間変化は図3を基に、図2の上部の赤線になります。
この期間を4つの波に分けて山火事理論を適用し、ブースター接種の抑制因子を入れて、データを再現するようにR0を決定し、自己無撞着な解を求めます。結果は図2の黒線です。左が線形表示、右が対数表示で死亡者も表示しています。ここで赤線の抑制因子を省いた解を求めます。図2の青線です。各波におけるブースター接種の抑制因子が時期的に異なることが重要です。
結果、第1波はほとんど変化しませんが、第4波ではピーク値で約83%の抑制効果が認められます。4つの波合計で感染者数は52%減、827万人の減少、死亡者数は28%減、4800人の減少の抑制効果が得られました。
最大18.3%の抑止因子で、感染抑止効果が大きく増幅されていますので、この結果の妥当性を他国の振舞いと比較して検討しました。
図4は、日本を含む、南アフリカ、米国、スペイン、オーストラリアの昨年12月から本年6月半ばまでの日毎感染者のデータと山火事理論の結果です。図3には、これらの国々の同時期のブースターの接種率も示しています。両者を比較すると、図4の5月以降の波のピークの上昇の割合は、図3のブースター接種率とよく相関しています。
接種率の小さい南アフリカ(5.6%)のピークが一番大きく、次に米国(36%)、スペインとオーストラリアは接種率がほぼ同じ(54%)で、ピークの上昇形状もほぼ同じです。日本が更に接種率が高く(61%)、ピークは形成せずなだらかな収束になっています。同じ図に、山火事理論で評価した日本のブースター接種がない場合の結果を橙色で示しています。
ブースター接種のほとんどない南アフリカほどには上昇しませんが、日本の場合、2回接種の発生予防の有効性が約30%残っていて、3回接種の有効性上昇が2回目から約30%であることを考慮すると、3回目の接種がない場合は、3回目の接種率が約半分、即ち約30%接種率の効果と同等であると見なすことができます。
これは、ほぼ米国の場合と同じになり、実際、橙色のピークの形は米国とほぼ同じ上昇のピーク形状です。以上より、山火事理論で評価したブースター接種の抑制効果、感染者総数で52%減は妥当であると考えられます。
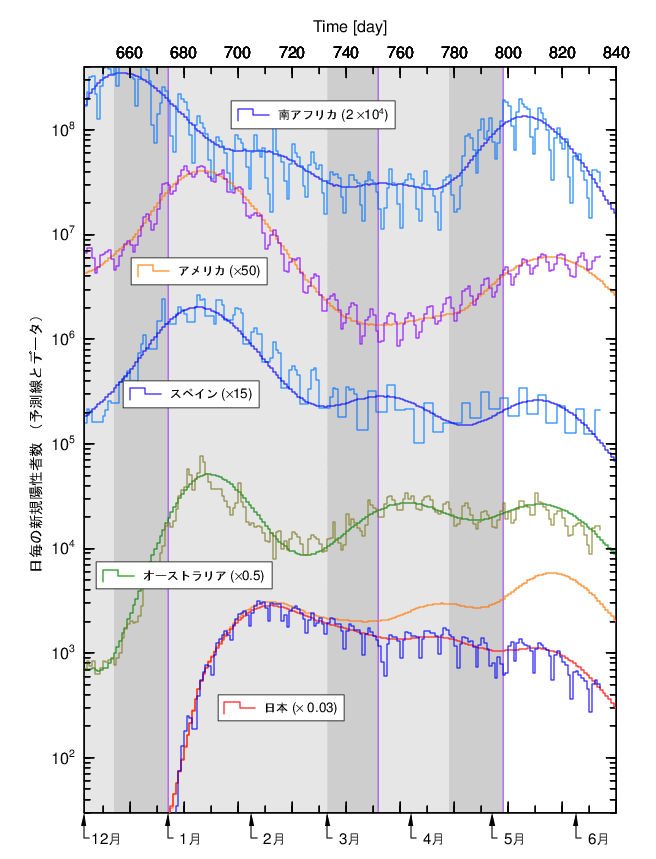
図4
謝辞
モンテカルロ法を用いてコロナ感染の解析を始めて2年半、本稿で50回なりました。この「アゴラ」に発表の場を得て大変励みになりました。面倒な理論と計算グラフであるにも関わらず、毎回快くこの場を提供して下さった編集担当の皆さまと、解析におつきあい下った読者の皆さまに感謝いたします。また、論文の作成にあたり、発想の転換の基となった山火事理論の提唱者である永江一石氏、中村幸嗣氏に改めて感謝を記します。














