たかが小学校の算数を語るのに、世界映画史に残る「2001年宇宙の旅」の話をするのも滑稽ではあるが、やってみよう。
2001年が、近未来どころか過去となった今見ても、新しい。
宇宙の果てに、何か知的存在(進化の果てに神になっているらしい)がいて、地球人類の英知なぞ、ヒトが次の階梯に進むまでの一時の毛布でしかないというストーリーである。
数学にもし、神と呼べる存在があるとしたら、それはあのホワイトルームのことである。
小2に戻ってみよう
小学校の算数の、こんな問題について考えてみよう。
ひとが6人います。全員にミカンを4つずつあげます。何個のミカンがいる?
数え方は二通りある。
① 皿1~6にミカンを順に1つずつ置いていくことを、4回繰り返す。(6×4=24)
② 皿1にミカンを4つ置き、次に皿2にやはりミカンを3つ置き、さらに皿6まで順にそうする。(4×6=24)
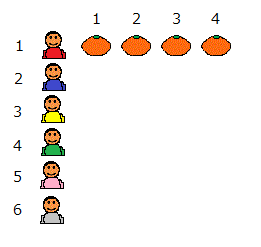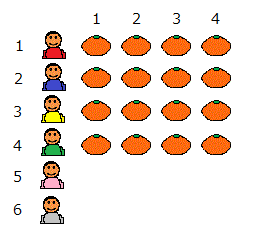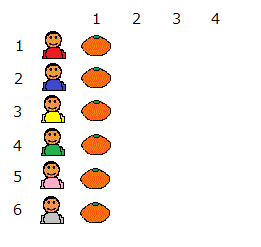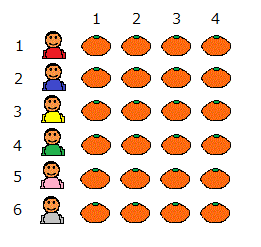
ミカンをどういう順に数えていくか、すなわち「時間の進め方」は、数えるひとの自由である。
しかし…
神には「時間」も「時間の進め方」もない。
なぜなら、過去も未来も今も、等しく眺めていらっしゃるからだ。
こんな風に。
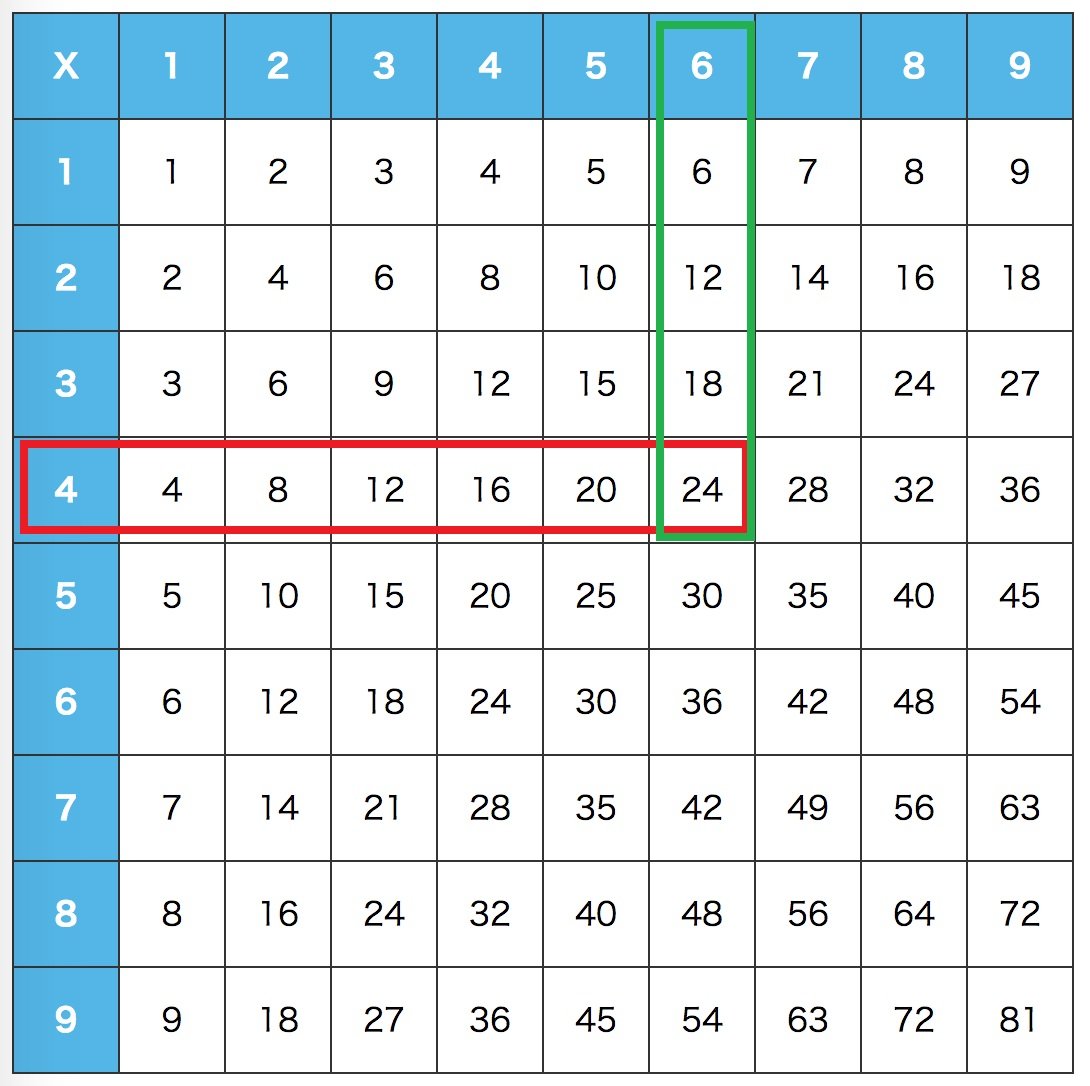
小2のとき、力づくでこの表を暗唱させられたことを、どうか思い起こしてほしい。
あれは、過去も未来も今もすべてお見通しの、すなわち時間という次元を超越した、数学という神の目線を、体験する最初の儀式なのだ。
小5にて
もうひとつ、小学校算数で、私たちはこんな儀式をくぐり抜けていく。
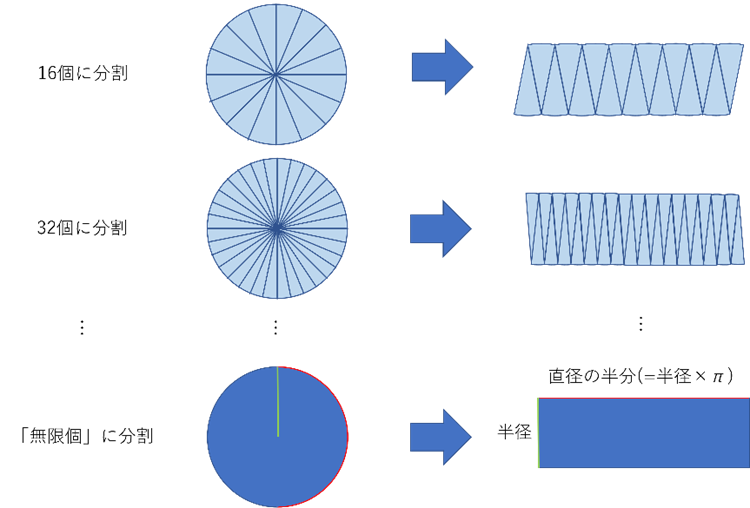
ホールケーキを、包丁でどんどん細かく切っていって、上下を入れ替えながら並べていくと、横長の四角形になっていく…
いわゆる円の面積である。
丸いケーキをどんどん細切りしていく… この説明には時の進みが(暗黙のうちに)内包されている。
そのため直観的に呑みこめる。
高校生になって、理系コースで数学を習うと、その終盤で、円の面積が再登場する。
それは微分・積分の最終ラウンドだ。
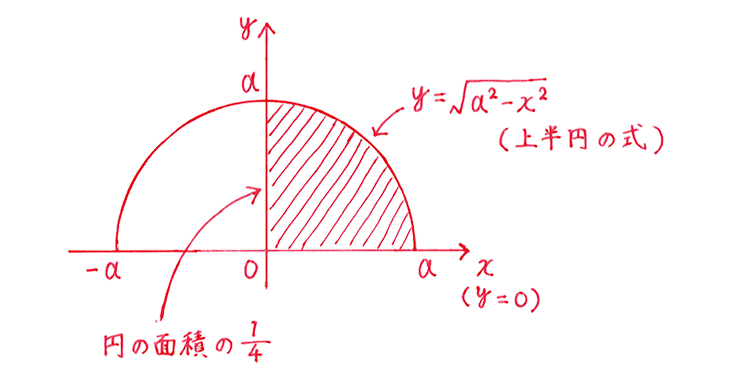
「小学校のときの級友と、高校卒業の前に再会を果たしたようだった」「ああきれいに輪が閉じた気がした」と、その時のことを振り返るひとは、受験数学の秀才たちである。
数学秀才たちは、こうして挫折していく
だがこうした秀才たちは、大学に進むと、やがて衝撃と失望を味わっていく。
ホールケーキを無限に細く切っていくという、素朴だが分かりやすい説明が、そこでは消えていく。
そればかりではない。
数を数えることさえ、消えていく。
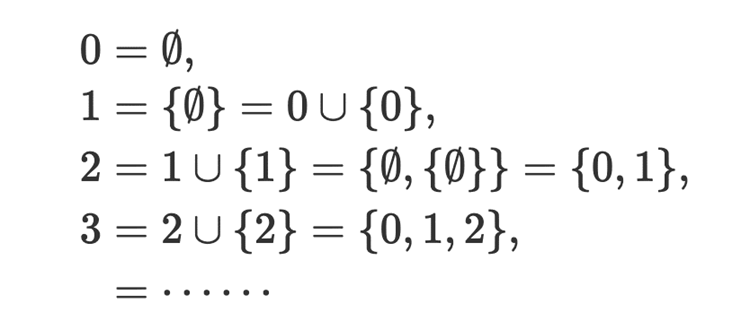
これが数(かず)であると、教えこまれる。
さんすうの基本である「ひとつひとつかぞえていく」は、消え失せるのだ。
数学秀才たちは、このとき思い知る。
俺は、あたしは、神の仕掛けた罠にはまったのだ、と。
映画「2001」のなかで、ヒトが、無限光の濁流に呑みこまれた末に、すべてが真っ白な部屋に、ひとり立ち尽くすように。
干からびた老人となって…
数学はBe動詞文である
どうして数学秀才たちがこんな目に遭ってしまうのかというと、厳密な話はここでは避けて、こんな風に説明しておこう。
私たちが小・中・高にかけて学んでいく数学と、大学以降の本格数学は、喩えるならばこんな英文の違いである。
① I teach English. (私は英語を教えている)
② I am an English teacher. (私は英語の教師である)
どちらも同じことを述べているわけだが、①は「teach」(教える)という動詞を使っているのに対し、②は「teacher」(教えるひと)つまり名詞を使っている。
動詞とは何か。そこに時の矢が伴うことばだ。
「教える」「持つ」など、そこには時間の経過が伴っている。
私たちが小・中・高にかけて学んでいく数学は、いってみれば動詞に頼った数文(英文ならぬ数文)である。
しかし大学以降は違う。
そこに広がるのは、動詞が禁じられた世界だ。「数学を学んでいる」と口にしても通じない、「数学学徒である」と言いかえると、ようやく音声センサーが作動してドアが開く、そんな無菌コンコースが連なって広がっていく。
「時間」が排除されたコンコース
この虚無とも無菌テントともつかない、真っ白なコンコース。その生まれは、日本でいう明治時代の前半。
ドイツの数学界での、ある論争を始まりとしている。
大御所クロネッカーいわく「整数は神の作ったものだが、他は人間の作ったものである」。
詳細は省くが、要するに数えることこそが、数学の基本であり、神がヒトに授けたもうた英知であるとする数学観である。
これに疑問符を付けたのがカントールという、当時の前衛数学者だった。
「数える」は、「時間の進み」という考え方を(暗黙に)数学世界に持ち込んでしまう。
それは人間の体感に基づくものであり、そういう即物的な考え方を、数学はむしろ排除していくべきではないか
体感や直観から、数学は独立を果たしていくべきだと、私は思う、と。
クロネッカーとカントール。これはどちらが正しい/間違いという論争ではない。どちらのほうが、今後の数学研究を、より広く、深く、豊かなものにしてくれるかの争いであった。
その観点でいえば、勝者はカントールであった。
無限、無限の無限、無限の無限の無限…
「時間の進み」を数学から排除し、代わりに∞(無限)を数の外縁に置く…
このアバンギャルドな方向性は、やがて「集合と写像」という、極めて抽象的な数学言語に結実していった。
「I teach English.」とあったら「I am an English teacher.」に訳さないといけない、冷徹な言語に。
スヌーピーの小学校にて
実は1960年代半ば、アメリカでそうした数学言語を、小学一年生から教えていこうという運動があった。いわゆる「ニュー・マス」(New Mass、新数学)。
どうなったか。スヌーピーのまんがでも揶揄されるような有様となった。
「こんなの2たす2もわかんなーい!」

(1965年10月5日付配信、チャールズ・シュルツ作「PEANUTS」より)
この波は、日本の小学校も呑みこんでいった。そして算数嫌いの子どもを大量に生み出すこととなった。
その反省から、1977年、学習指導要領の改訂で、ニュー・マスへの決別が宣言された。代わって「ゆとり教育」が訴えられた。「ゆとり」というと平成のイメージだが、実際はこの昭和52年生まれである。
事の顛末については、算数教科書の老舗出版社の、公式サイトより引用しておく。
世界的な規模で展開された現代化運動でしたが、学校現場では、集合などの新しい内容や過多な学習内容に対するとまどいも少なくありませんでした。しだいに、マスコミからも「落ちこぼれ」などのことばで現代化批判がなされ、またアメリカでは「Back to the Basics(基礎・基本に帰れ)」運動が広がりを見せるようになります。
こうした流れのなかで昭和52年に改訂された学習指導要領では、「ゆとりと充実」がキーワードとしてかかげられ、基礎的な知識・技能を重視し、基本的な概念の理解を目指すため、学習内容が精選されました。
昭和55年小2
戦前昭和と戦後昭和のさんすう
ここで掛け算の順序論争に話が戻る。
私は当初、ニュー・マス導入とその破棄の混乱の落とし子として、こうした掛け算順序論争が生じたのだろうと想像していたのだが、日本の算数教育を(各時代の算数教科書にも目を通しながら)探っていくにつれて、根はもっと深いことに気づいていった。
これはむしろ戦前昭和の算数と、戦後昭和の算数の、権力争いの落とし子らしい、と。
この両者の違いは、簡単に言うと「前者は暗算重視/後者は筆算重視」にある… ときれいにまとめてしまいたくなるのをぐっとこらえて、両者には、ある共通点があることを指摘しておこう。
アメリカ算数への強い反発心だ。
ご承知のように、今の小1、小2には「せいかつか」があって、小3より理科と社会に分岐するのだが、日本の敗戦後、アメリカから持ち込まれたのが、理科、社会それに算数を一体化させたような小学校カリキュラムであった。
当時のアメリカ教育学の最新理論を、日本で実践するという、理想の光に満ちた試みであったが…
児童の算数力の、著しい低下を招いてしまった。
その後、日本が独立を回復すると、アメリカ占領下では戦犯扱いだった戦前の算数教科書チームが息を吹き返し、文部省とも歩調を合わせていった。
だが一方で、戦前算数の復古について、アメリカ算数と等しく批判する派が台頭していた。
タイルを黒板に並べて計算していく、そういう算数を習った向きも少なくないだろう。あの教え方は、この新派によるものだ。
数を重視する戦前復古派と、むしろ量を重んじる戦後新派…
奇しくもクロネッカーとカントールの論争と、相似形となった。
文部省と日教組の対立構図とも、次第に重なってしまった。
「算数論争は教室の外でどうぞ」
さらにはニュー・マス騒動の後遺症にくわえ、日本の国際競争力の変動と、その対応策として、算数教育(というか算数カリキュラム)の大幅変更が、国の主導で繰り返される。
そうした教室外での暴風雨に、現場の教師たちがついていけなくなった。
教室の窓を閉め切って、算数の基本マナー作りに傾いていった。「これが社会人の、正しい名刺の渡し方です」の小学生版として…
これが掛け算の順序、いわゆる「超算数」とも揶揄される、小学校算数マナーの誕生と定着の経緯である――異論もあるだろうが、そう的外れでもないと、自分は考える。

takasuu/iStock
日本の算数
ところで「2001年宇宙の旅」には、サルがヒトへの道を歩みだすとき、そしてヒトがそれ以上の存在に気づくとき、大きな黒い石板(モノリス)が現れ、行く手に立ちはだかる。
ものいわぬ導師として、ヒトをサルから導きあげ、さらにその先に招いていく。
少なからぬ犠牲者も出しながら。
実は日本の算数教育についても、あのモノリスのまがい物が働いている。
それも悪用されて、だ。
(つづく)













