仁井田 浩二 RIST(一般財団高度情報科学技術研究機構)、理学博士
コロナ感染拡大と収束の重要なポイントをおさらいします。
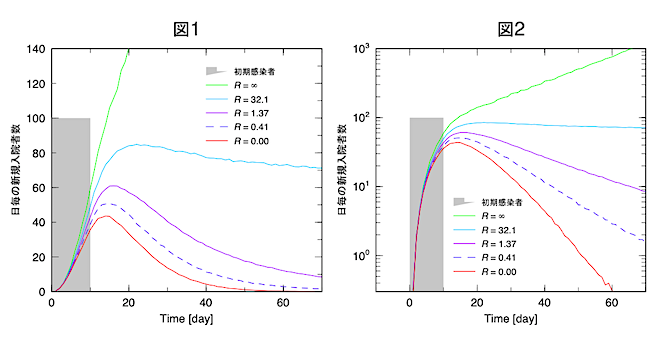
図1は、連載④で用いたものですが、図2は図1の縦軸を対数表示したものです。この図に示されているのは、毎日100人の感染者が10日間入国し、その後、国内の病院で報告された日毎の新規感染者数です。赤線は感染力(R)がゼロの場合、即ち、全く他人に感染させなかった場合です。
この場合ですら、病院で報告される患者数だけを見ていると、急激な感染拡大が起こり、そして収束していったように見えますが、感染はありませんから、病院に訪れたのは入国した感染者だけです。このシミュレーションでは、感染者は1週間で発病、更に1週間で入院、そこから2週間で回復もしくは死亡というモデルを確率論的に扱っています。その結果が赤線です。個人の中だけで起こる事象で、分布はポアソン分布になります。
感染で新規感染者が発生します。その感染者も個人的事象としては、赤線と同じ振舞いをします。即ち、感染によってポアソン分布を示す個人が多数発生し、その重ね合わせとして、図の青や紫、緑の線が決まります。感染力(R)の大きさによって、感染者数が増大します。特徴は、図2が示すように収束の傾きがRによって変化し、逆にこの収束期の傾きからRを推定することができることです。
このモデル(連載①)では、感染力(R)は、σρβの積で決まります。σは接触する確率、ρは人の密度、βは感染確率、ですが、モデルの中では、3つのパラメータの積でしか登場しないので、これらの積の値を変えて感染力を変えています。σρβの積の値を決めたときに、ひとりの人から何人の人が罹患して入院したかという数を実際にシミュレートして求めたのがRで、このR値を感染力の強さの指標として使います。
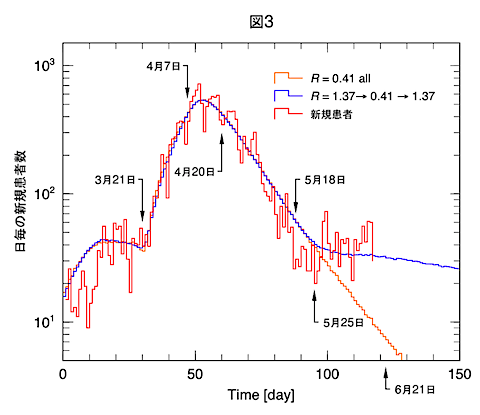
図3に6月16日までに報告された新規感染者(赤)を示しています(縦軸は対数表示)。5月25日以降の感染者数の動向は、それ以前の傾きから大きくずれました。これは連載③で示したように社会の感染力(R)が変化した、つまり自粛の効果はあったことの証です。
収束期の傾きはRで決まります。4月20日から5月25日までの傾きはR=0.41でフィットされます。5月25日以後の傾きをフィットした結果はR=1.37です。(最近の新規感染者数には空港の入国者でPCR検査陽性の人が含まれていますが、厚生省のデータからそれらの人数を省いてあります。)この自粛解除後の感染力R=1.37を日本社会の持つ基本的感染力だと仮定し、4月7日の自粛以前にもこのR値を使います。
図3の橙線は自粛の効果を考慮せずR=0.41を全期間に使い5月30日までのデータをフィットしたものです。もうひとつの青線は、R=1.37で始まり、4月7日の緊急事態宣言から自粛の効果でR=0.41に減少させ、自粛を5月18日に解除してR=1.37に戻した結果です。両者とも5月25日まではよく一致していますが、自粛解除の影響が5月25日以降の振舞いに表れます。
K値を用いて、自粛の効果の有無を論じることがされていますが、5月25日までの結果を用いて自粛の効果の有無を判定することは不可能です。シミュレーションの結果が示すように、自粛がある場合と無い場合、5月25日までの結果はほぼ同じ値を与えますから、それらからK値を導出しても差はありません。5月25日以降の変化から判定することはできるかもしれませんが、それはここでやったことと同じです。
以上の考察から、自粛前の社会の基本的R値(=1.34)も決定できましたので、自粛の効果をシミュレートします。これからがシミュレーションの醍醐味です。
自粛の効果を見るために、自粛無の場合、解除の日を変えた場合、そして最後まで解除しなかった場合についてシミュレートし、患者数、死者の結果を表1で、日毎の新規患者数の変化を図4、図5(縦軸対数)に示しました。
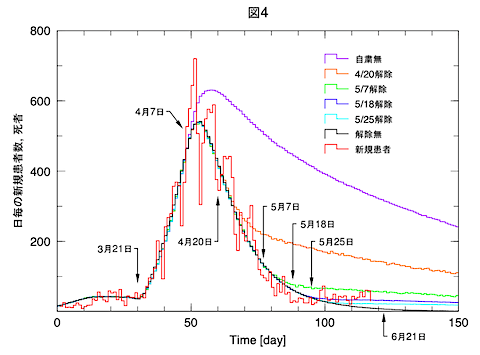
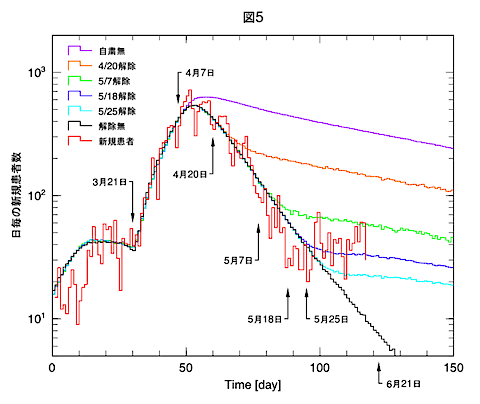
表1
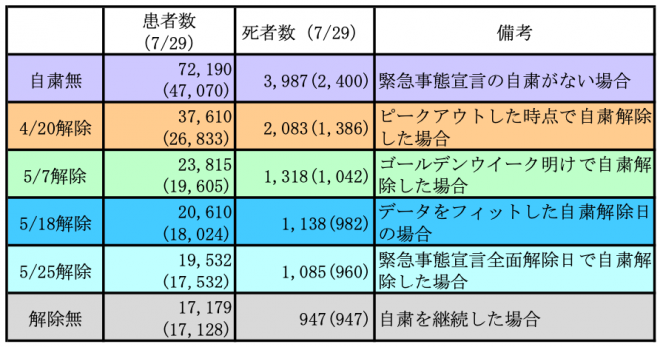
表1の患者数、死者数は、2年後(730日)の予想数、カッコ内は本年7月29日時点での予想数です。6月16日現在、日本全国の患者数は17,601人、死者は929人です。自粛が行われなかった場合、現在の状況の約4倍弱の患者、死者数になります。
ピークアウトした時点で自粛解除すべきであった、もしくは、ゴールデンウイーク明けで自粛解除すべきであった、という意見も出ていましたので、それらに対応した場合も計算してみました。42万人のような評価には使えそうもない数字ではなく、これらは具体的に自粛の効果をいろいろなケースで評価するのに使える数字だと思います。
さて、今後です。これまではほぼ鎖国状態でしたが、これからは徐々に他国との交流を再開しなければなりません。毎日10人の感染者の入国が3ヶ月続くと再び爆発的感染拡大になるという予想もあったので、このモデルで確かめてみました。
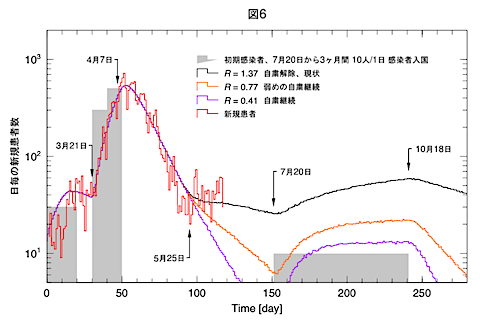
図6は、7月20日から10月18日まで3か月間、毎日10人の感染者(未発症者)が入国した場合です(グレーの領域で表示)。黒線が5月18日以降、自粛解除したR=1.37(黒線)の場合です。参考にR=0.77(橙線)とR=0.41(紫線)の結果も載せています。
R=1.37(黒線)の結果では、新規感染者が徐々に上昇して3ヶ月の終わりには、一日58人に達します。7月20日の時点で26人の感染者ですから、3ヶ月経った段階で日毎22人の新規感染者(10人は入国感染者)が報告されます。この後も入国が続けばこの人数は増え続けます。また、感染者の入国者の数が倍になればこの数も倍になります。今後の入国制限の緩和は、難しい問題ですが、これらの予測値が制御の方針、実態把握の指標として重要だと思います。
世間では、緊急事態宣言による自粛の是非を問う議論が多くなされています。紛糾の原因は、自粛を行わなかった場合の結果が分からないことです。そこでモンテカルロシミュレーションを用いて自粛を行わなかった場合を計算し、自粛の効果を定量的に評価しました。自粛の効果はあったというのが結論です。自粛の効果を数値によって把握することがまず大事です。それによって、自粛による感染抑制の効果と、自粛に伴う費用の具体的な検証が可能になります。第2波、第3波の感染に今回と同様の膨大な経済的損失ともなう自粛の全てを繰返すわけにはいきません。















