税収の見積もりは簡単か？

「税収の見積もり」は財政・社会保障改革と経済成長のあり方を巡って重要な役割を担うが、最近、その見積もりが簡単であるかのような意見を時々伺う。確かに、消費税は経済動向に左右されない税収であり、所得税や法人税については、「好景気＝税収増」「景気低迷＝税収減」という傾向がある。しかし、通常の税収見積もりは極めて難しいのが現実である。

その理由のカギは、「税収弾性値」という概念が握る。税収弾性値とは、名目GDPが1％成長したときに、税収が何％増加するかを表す指標である。例えば、税収が1.2％増加するとき、税収弾性値は1.2であるという。このとき、税収弾性値εの定義から、以下の関係が成り立つ。

　税収の伸び＝ε×名目GDP成長率　　　・・・(＊)式

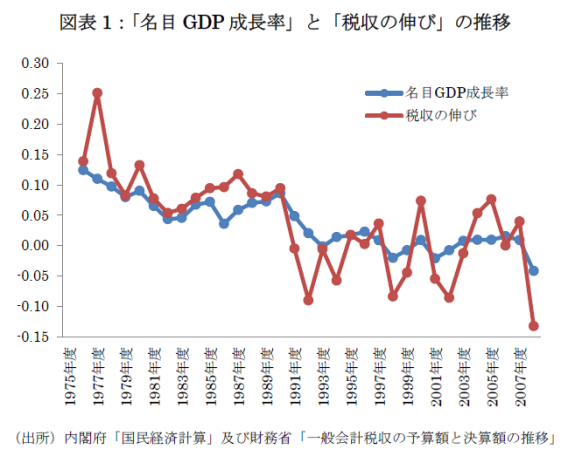
この(＊)式において、もし税収弾性値εが安定的であるならば、原則として、「名目GDP成長率」と「税収の伸び」は同じ動きをするはずである。この確認のため、政府の公式データ（1975年度―2008年度）を利用して、名目GDP成長率と税収の伸びの推移をグラフ化してみたものが以下の図表1である。

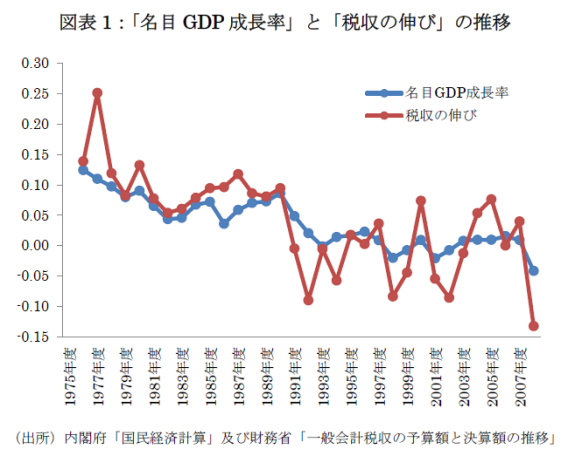
まず、このグラフから読み取れることは、大雑把には、成長率と税収の伸びは似た動きをしているということである。しかし、バブル崩壊後の1990年度以降において、この構造は変化している可能性がある。

というのは、1990年度以前では、「税収の伸び＞成長率」の傾向（つまり、税収弾性値＞1）をもつ。だが、1990年度以降では、税収の伸びが成長率の周りで大きく乱高下し、「税収の伸び＜成長率」となる期間が頻繁に表れているからである。

もちろん、バブル崩壊後には、1997年に本格化する金融危機の影響などもあるから、完全に構造が変化してしまったとは断定できないが、税収弾性値がかなり変動している可能性がある。

そこで、この様子をみるため、図表1のデータについて、横軸に「成長率」、縦軸に「税収の伸び」をプロットしたものが以下の図表2である。

図表2において、各プロット点と原点Oを結ぶ直線の「傾き」が税収弾性値εに相当する。もし傾きが1以上の値であるならば、経済成長のスピード以上で、税収が増加していることを意味する。逆に、傾きが1よりも小さい値であるならば、税収は経済成長のスピードよりも低い形でしか増加していないことを意味する。

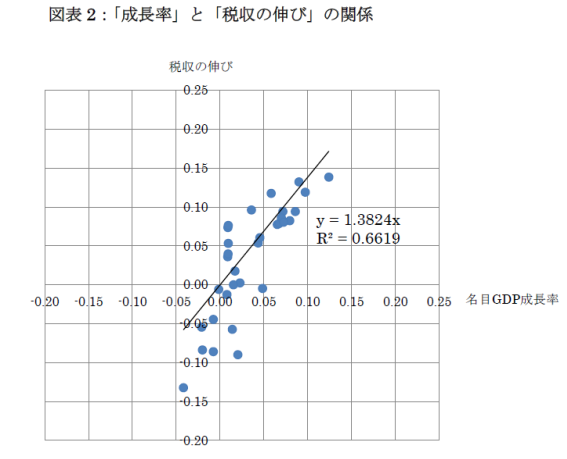
また、図表2に描いた直線は、原点Oを通過するプロット点の回帰直線である。この直線の傾きは1.38であるから、税収弾性値εは1.38と結論づけることはできない。

というのは、回帰直線の説明力（R^2）は66％しかなく、この直線の周囲にプロット点がかなりバラついているからである。しかも、各プロット点と原点Oを結ぶ直線の傾きには、マイナスの値のものも多く存在する。これは、税収弾性値εがマイナスであることを意味する。

財務省の税収見積もりや内閣府のマクロ経済予測などでは、税収弾性値を1.1として推計することが多いが、現実には、税収弾性値εは不安定である可能性が高い（なお長期の税収弾性値は理論的に1である）。

さらに、実際は成長率の予測もなかなか難しい。このため、(＊)式において、「税収の伸び」は「税収弾性値」と「名目GDP成長率」の積であるから、実務上、税収の見積もりは極めて難しい作業となるのである。

（一橋大学経済研究所准教授　小黒 一正）