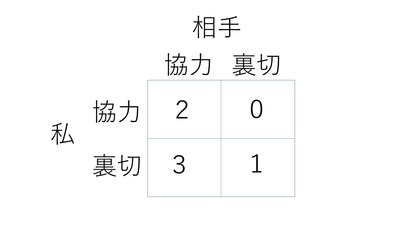
経済学のことばで、ほとんどの人がまちがって使うのが「囚人のジレンマ」です。多くの人はなんとなく板ばさみになった状態を囚人のジレンマと呼んでいますが、これはジレンマではありません。それはゲーム理論のことばで、次の図のようなゲームをいいます。
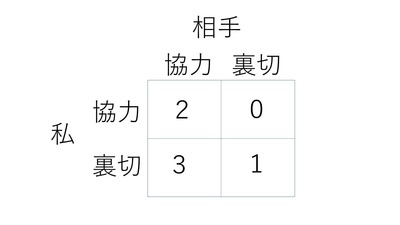
ここでは私と相手は対称と考え、私のペイオフ(得点)だけを描いています。この図は「相手が協力した場合に私が協力すると私のペイオフは2だが、私が裏切ると3」と読みます。同じように相手が裏切ったとき私だけ協力すると0ですが、私も裏切ると1になります。これは私と相手を入れ替えても同じとします。
このとき、私はどう行動するのが合理的でしょうか? 相手が協力するなら私だけ裏切ったほうが得だし、相手が裏切るなら私も裏切ったほうが得ですから、どっちにしても裏切ることが合理的ですが、2人が裏切ると1ずつしかもらえません。2人が協力すると2ずつもらえるのに、それは合理的な解としては実現しないのです。
これはジレンマではありません。囚人というと互いに密閉されていないと成り立たないようですが、話し合っても同じです。「私は協力します」といって裏切ることはつねに合理的だからです。つまり裏切ることは相手の出方に関係なく最適なので、悩む必要はないのです。
これについて、いまだにアクセルロッドの「しっぺ返し」が最強だと信じている人がいますが、まちがいです。それは1対1の特殊な状況だけで成り立つ結果で、多人数ゲームではつねに裏切る戦略が強いのです。
では、この裏切りを避ける方法はあるのでしょうか? 1回かぎりのゲームでは互いに協力する解はありませんが、同じゲームが無限回くり返されるとすると、協力を実現する方法があります。図でいうと、相手が協力した場合は協力し、裏切ったらこっちも裏切り続けると、協力が成立します。
ごく簡単にいうと、最初に相手が協力して私が裏切ると私のペイオフは3になるが、次から相手が裏切ると両方ともペイオフは1になります。これに対して両方が協力を続けると双方ともずっと2だから、私の長期的な利益は3回目で
裏切り:3+1+1=5
協力:2+2+2=6
となるので、3回以上ゲームをくり返すと協力のペイオフのほうが大きくなります。無限回だとちょっとむずかしい計算になりますが、ゲームが十分長く続くと協力のほうが大きくなります。このように囚人のジレンマでも長期的関係が強いと協力が実現するというのが、ゲーム理論のおもしろい結果です。
これは日本の会社にも当てはまります。1回ごとにやとわれるアルバイトは残業しませんが、「正社員」のおじさんは命令されてもいないのに遅くまで残業します。それは日本の会社が長期的関係で結ばれた共同体で、一度でも会社を裏切ると「村八分」になって左遷されるからです。これは「ものづくり」に役立つこともあるのですが、電通事件のような悲惨な結果になることもあります。