1.西浦氏の予測
久しぶりに西浦氏が感染拡大についてシミュレーション結果を公開しています。本日は、まず氏の結果から議論します。

Amazonより:編集部
西浦氏は、「予測」という言葉は不適切と考えておられるのか、「プロジェクション」と表記されています。例えばモデルがしっかりしていて、後は幾つかのパラメータを変えて結果を比較するためだけなら良いのですが、モデルに含まれる確立されていない仮定が大きく結果を変えるレベルであるならば、やはり「予測」、もしくは本連載で使う「短期予報」の方が適していると私は考えています。
まず西浦氏の結果を見てみましょう。図1は東京都の陽性者数です。昨年4月の氏の示した結果より格段に現実的な予測になっています。
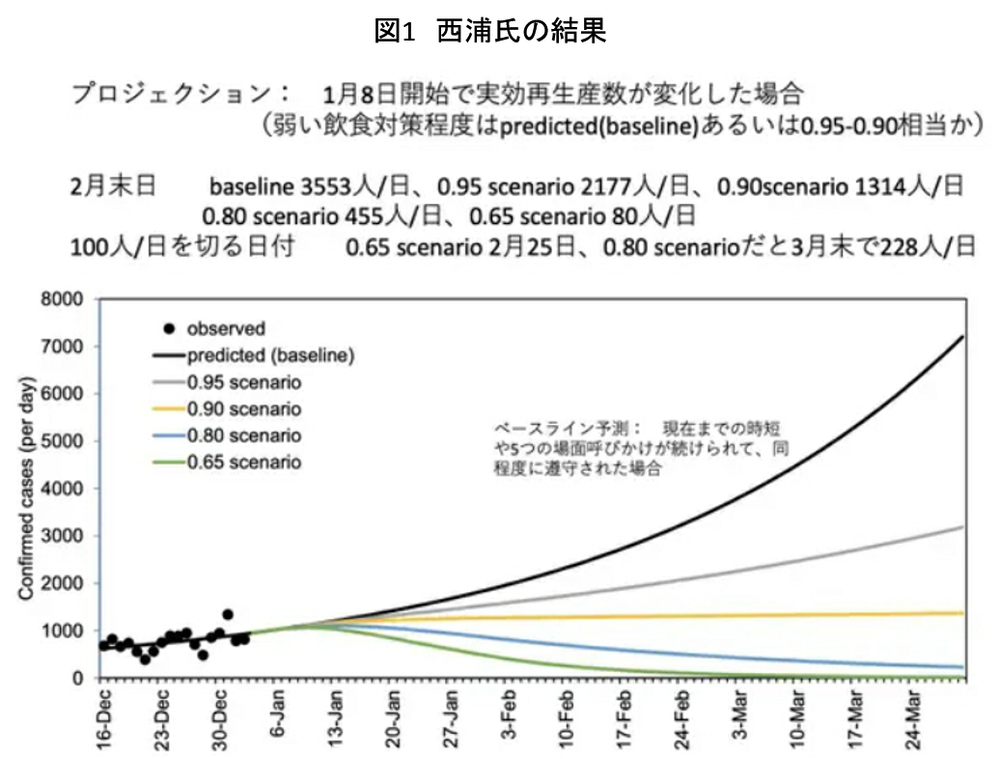
氏の今回の解析の仮定は、(1) ピークアウトの設定を1月8日に固定。(2) 収束はRt(実効再生産数)を変えてケーススタディ。(3) Rtは、人々の行動変容の関数として変化する。というものです。人々の努力によってRtが変わり、それによって収束までどのくらい時間がかかるかケーススタディをした、ということでプロジェクションということのようです。
本連載の私の最新の結果を示します。図2では、5種類のピークアウト日を設定しています。(1) ピークアウト無、(2) 1月28日、(3) 1月14日、(4) 1月7日、(5) 12月31日と変化させた結果を示しています。元旦の解析では、12月22日のピークアウトを設定しましたが、本日(1月7日)のデータを見ると、1月14日くらいにシフトしないとこの急上昇を再現できません。
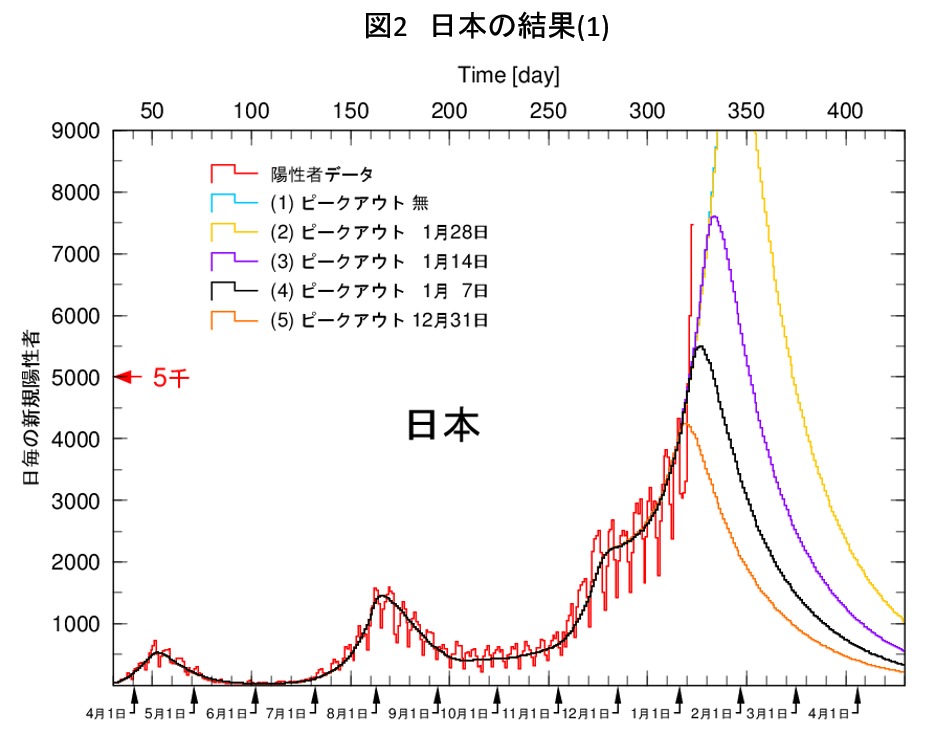
図1と図2では同じようなことをやっているのですが、図から受ける印象は全く違います。そこで、図2を図1のスケールに合わせてみましょう。そうすると図3になります。図3では、西浦氏に倣って、2月末日の陽性者/日、死亡者/日と、全国での陽性者/日が1000人を切る日を示しています。
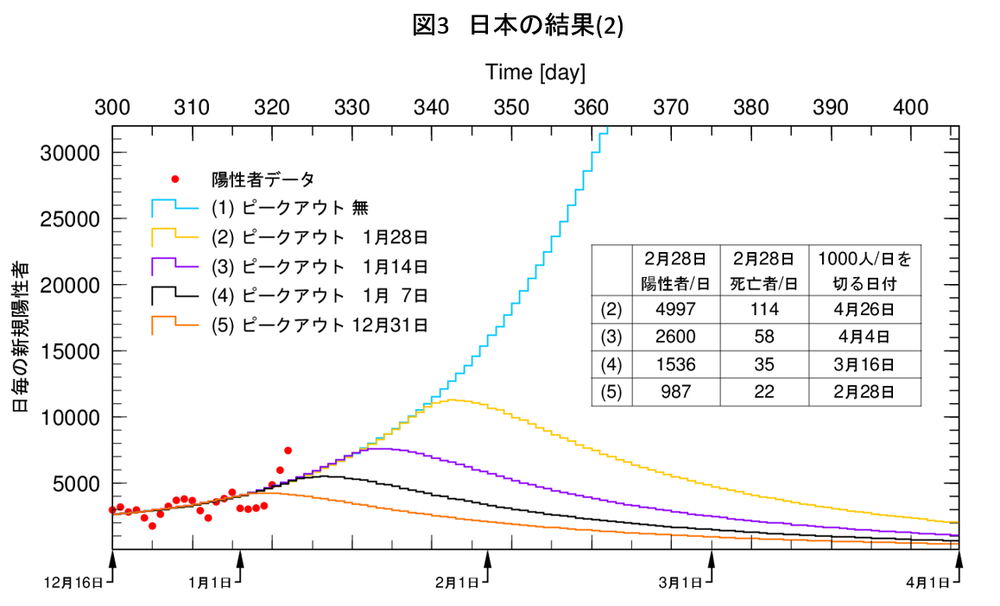
図1は東京で、図3は日本です。ほぼ同じようなグラフに見えますが、両者の振舞いは甚だしく違います。次の図4は、私のモデルで西浦氏の仮定を実行した結果です。即ちピークアウトの日を1月7日に固定して、収束時のRtを0.78、0.94、1.00と変化させた結果を図2と同様に、これまでの表示の仕方で示します。
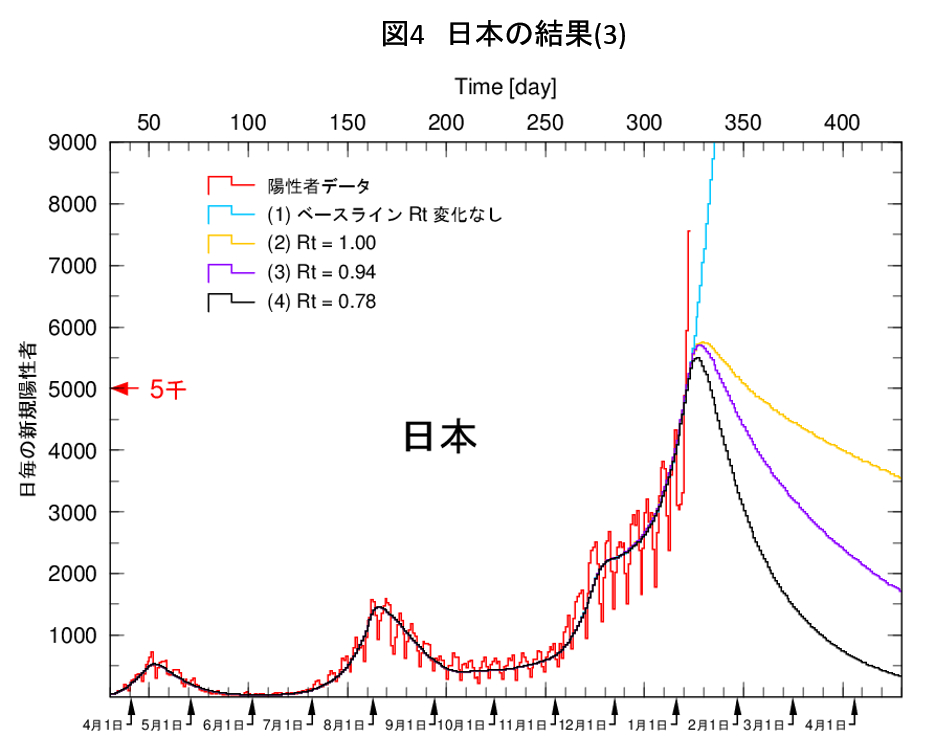
図2と図4を比較すると、両者の仮定の違いが明確になります。両者の違いは、図4の西浦氏の仮定は、ピークシフトの日は固定して、下降部のRtを変化させている、一方、図2の本解析では、上昇部と下降部のRtは固定して、ピークアウトの日だけを変化させている、という点です。
両者とも、ピークアウトするメカニズムは、モデルとして持っていませんから(SIRモデルの「免疫によるピークアウト」は除く)、ピークアウトさせるには仮定が必要です。西浦氏は、人々の行動変容によるRtの変化という仮定をしています。本解析では、これまでの解析からピークアウトの原因は分からないものとして、現象論をとっています。即ち、データを再現するようにピークアウトの日付を設定しています。
昨年5月末頃は、私もアゴラの連載③で、緊急事態宣言の解除時に、西浦氏と同じような図を書き、Rtの変化によるケーススタディを行いました。自粛の効果を評価するためです。解除後、陽性者が増加したため自粛の効果が「あった」と判断しました。自粛の効果がなければ、解除後も自然減少するはずだと考えたからです。実際には新しい波が来て増加していたのですが、現象論ですので自粛の効果と判断せざるを得ませんでした。
しかし、これまでの解析で、特に第1波の死者、実効感染者のピークの半値幅(ピークのところから半分の高さの山の幅)は、ほぼ全ての国で同じであることが分るようになりました。図5に、9カ国の実効感染者の日毎変化を、第1波のピークの値を100人に規格化し、ピーク位置を50日目にシフトして重ねたグラフを示します。アメリカやスウェーデンのように多少広がっている国もありますが、それ以外は見事にピークの形、半値幅が一致しています。
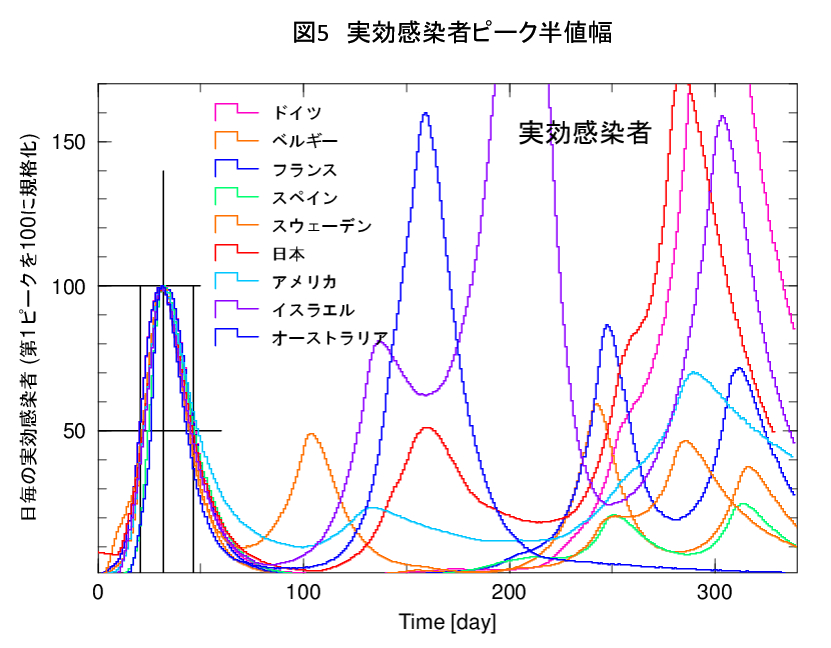
第2波、第3波についても、第1波ほどではありませんが、半値幅が同じレベルであることが分ってきています(図5の第1波の波の振舞いに表れています)。絶対値は100倍以上の差がある国々で、また、ロックダウン等の対策が様々である国々において、第1波の半値幅が同じで、ほぼ1ヶ月で収束しているというのがデータから示された事実です。
この事から、ロックダウンや自粛の効果は、ピークの高さには各国の対策の違いが大きく表れるかもしれませんが、ピークの幅にはあまり影響を与えていないことが分ります。そこで、ピークアウトを予測するときに、我々は上昇期、下降期のRtはそれぞれ一定にして、Rtが変化するピークアウトの日付だけを変化させる方法を取っています。
西浦氏の仮定ですと、各シナリオでピークの幅がどんどん変わりますが、我々の仮定ですとピーク高は変わりますが、ピーク幅はほとんど変わりません。これまでの多くのデータを考慮すると、より現実に即した仮定であると考えています。
2.シミュレーションのV&V(Verification and Validation)
本解析で用いているモンテカルロシミュレーションコードPHITSは、本来放射線輸送現象を解析するためのコードで、いろいろな研究分野で使われています。原子力施設等の放射線安全評価では、許認可のための資料にもなりますので、コードの検証と妥当性確認(V&V)が行われています。また、工学系で用いられる多くのシミュレーションコードについては、V&Vのための方法論、手順書等も整備されているのが普通です。
シミュレーションには危険なところがあります。インプットを入れると答えは必ず出てしまいます。新型コロナ関係でも、バーチャルリアリティ的なシミュレーションがたくさん出てきて、感染拡大に対する様々な効果が評価されています。問題はそれらの解析のV&V、特に妥当性確認が行われているかどうかです。
例えば、人と人の接触を減らせば、感染防止になるのは自明です。ただし、ある特定の接触の抑制が、全体の感染拡大にどのくらい効果があるかを評価するのは難しいことです。少なくともこれまでの陽性者、死亡者の推移を再現していることが最低条件で、その上で、その効果が全体の中で、何%なのか、また、それを検証できるデータは何か、ということを明確に、結果として公表しなければなりません。
西浦氏は、氏のモデルで過去のデータが如何に再現されているか、もしくは、それができていないのかを明確に示す必要があります。また、今回の結果で具体的に指摘すると、西浦氏の図1では、彼がベースラインと言っている線が、これまでのデータを再現しているかどうかが図1では判別できません。図1と図3を比較すると、その差がはっきりしませんが、図2と図4で比較すれば、両者の仮定の差がはっきり分かりますし、データとの詳細な検証ができます。これらは、グラフの横軸の範囲と縦軸のスケールの問題です。
また、シミュレーションの信頼性確保という点では、予測性能のロバスト性(頑強性)を考慮する必要があります。陽性者の推移だけを再現するシミュレーションは比較的簡単です。しかし、それと同時に異なるシナリオに基づいた同等の結果を与えるシミュレーションが可能となってしまいます。そのため、観測量として、死亡者の推移、年齢別の感染者、死亡者、等を加えて、シミュレーションの信頼性の確保・向上に努める必要があります。
昨年5月にこの連載を始めたきっかけは、数理感染学という分野があることを知った驚きと、そこで示されたシミュレーション結果が、全くベンチマーク等の結果の妥当性確認がなされていないことでした。批判する以上は、検証可能なデータの出し方に注意してきましたが、これからも、新型コロナ対策に役にたつ解析に寄与できればと考えています。













