
udra/iStock
(モンテカルロシミュレーションで検証 連載39)
本稿では、ピークアウトのメカニズムとして、(1) ワクチン効果、(2) 免疫効果(永江一石氏、中村幸嗣氏の山火事理論を含む)所謂集団免疫効果、そして、前回考察した(3) ウイルス自滅効果、の3つの仮説について検証します。

図1は、日本の陽性者、死亡者の推移です。左図上が実効再生産数(簡易式)Rt、左図下が陽性者、死亡者の線形表示、右図が対数表示です。
この図からまず分かることは、第何波と呼ばれるピーク構造です。ピーク値の大小はありますが、きれいな周期性を示し、世界的に見ても同期している同様なピーク構造が見られます。このピークアウトの主因を掴むことが、コロナ対策として最も重要です。
今回注目するのは、デルタ株のピークアウトです。特に日本の第5波のデルタ株がピークアウト後、極めて急激に収束を続けたという事実を取り上げます。
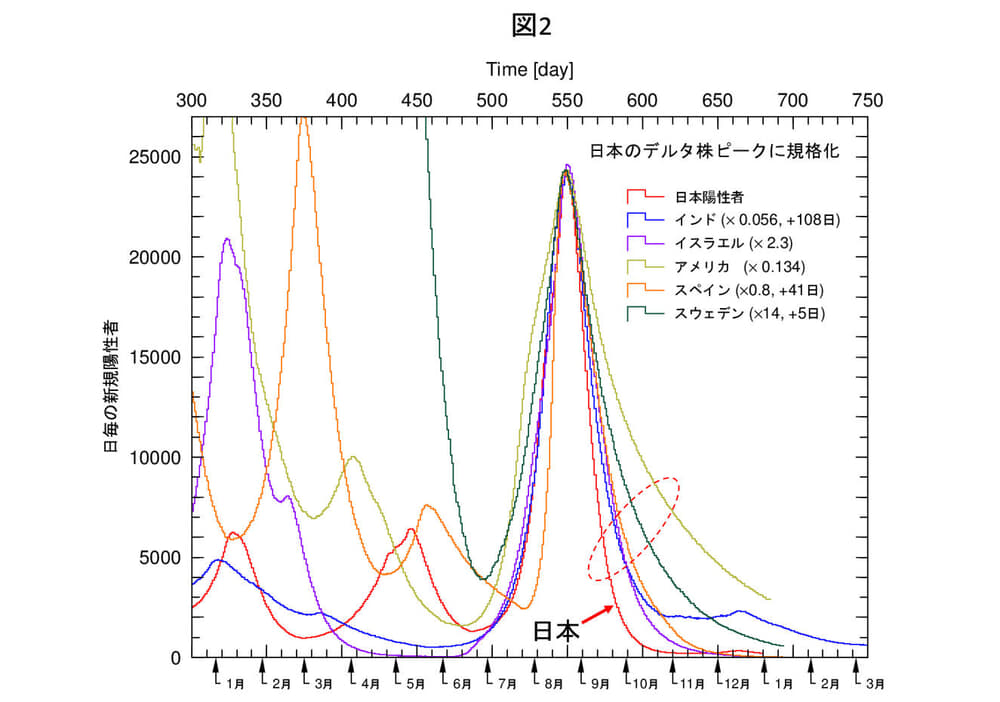
図2は、解析を行っている6カ国のデルタ株をピーク位置で規格化したものです。図中の破線楕円で示した領域、即ち収束期の幅、これに注目します。現実問題として、このようなピークの幅を拡げる要素はいくつもありますが、狭める要素はほとんどありません。日本はこの中では一番狭い幅を示していて、ピークアウトのメカニズムを検証する上で非常に重要なポイントです。
1.方法論
ワクチン効果、免疫効果、ウイルス自滅効果、それぞれの効果をモンテカルロシミュレーションに実装し、日本の第5波のデルタ株のピークの上昇部を再現するように感染確率を決めてシミュレーションを行います。
その結果、それぞれの効果でピークアウトした後の収束部がどのよう形になるか、狭い幅のデータを再現できるかどうかを検証します。
2.ワクチン効果
ワクチン接種率は日本の2回接種のデータを使い、感染抑制効果の発現は、接種後2週間と仮定して、データを2週間後方シフトしています。また、感染抑制率は90%とも60%とも言われていますが、ここでは100%と70%の2ケースを仮定します。現在2回接種率が国民の71%位ですから、ワクチン効果(接種率×抑制率)は、0.71(=0.71×1.0)と0.5(≒0.71×0.7)が最大値になります。(1.0-ワクチン効果)が感染確率へのワクチン効果の因子になります。
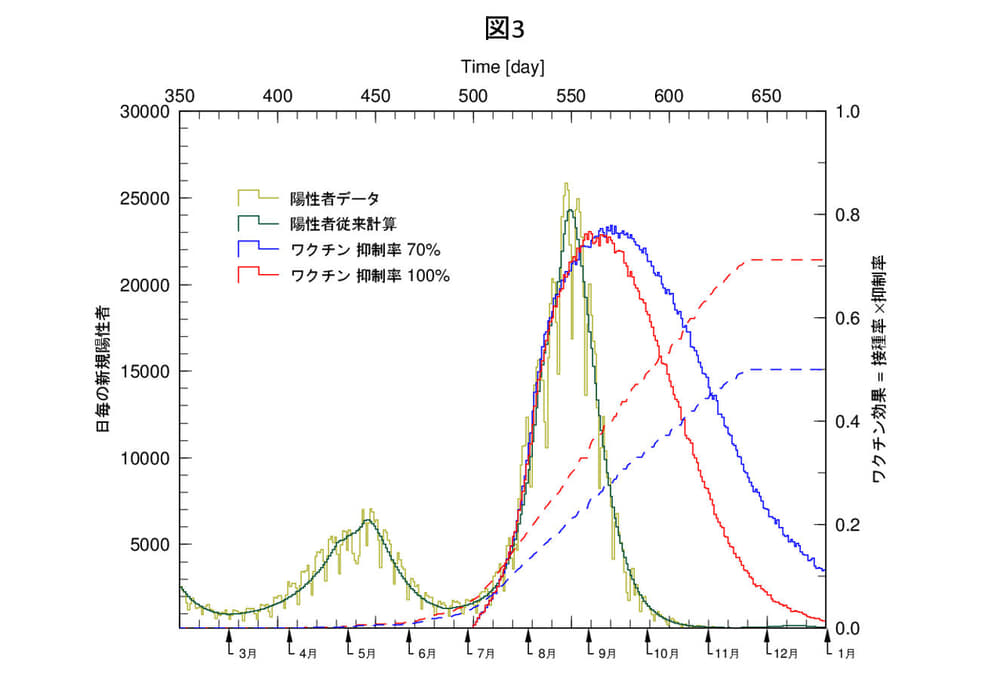
図3にワクチン効果によるピークアウトの結果、抑制率が100%(赤線)、70%(青線)の結果を示します。いずれの場合も、ワクチン接種の増加が感染拡大と重なったため、その効果でピークアウトはしましたが、鋭いピークと急激な収束は全く再現できません。ワクチン接種の効果がデルタ株のピークアウトの主因ではないことを示しています。これは、ワクチン未接種であった第1波から4波でもピークアウトが起きていることからも分かります(図1参照)。
3.免疫効果
SIRモデル等で用いられる集団免疫効果です。罹患した人が免疫を獲得し、その人数が増大すると罹患できる人が減少するので、その効果で感染拡大がピークアウトし収束するというメカニズムです。この仮定は、ワクチン効果に比べると、罹患した人数にリンクして感染抑制が働くので、ピークアウトのメカニズムとしては魅力あるものです。
問題は母集団の人数と罹患した人数の関係です。今回計算では、デルタ株での陽性者数は約85万人です。これは日本人口の僅か0.7%です。これでは集団免疫効果は期待できません。永江、中村山火事理論では、「感染爆発が起きると、燃えやすいところが燃え尽きることで周りに弱いながらの自然感染免疫ができて収束する。結果、一過性の集団免疫のような状態になる」という仮説です。
これはローカルな集団免疫が効果を発揮するという理論と解釈でき、シミュレーションでは、罹患できる母集団の数を限定的に仮定して、罹患した人は免疫を獲得し、結果、罹患できる人数が減少し感染抑制につながるという計算モデルにしました。

図4は、母集団の100%が感染者総数とした場合(母集団85万人、赤線)、母集団の80%が感染者総数とした場合(母集団106万人、橙色)、50%とした場合(母集団170万人、青線)の結果です。破線で示したのが、免疫獲得率、即ち、免疫を獲得した人数の設定した母集団に対する割合の推移です。(1.0-免疫獲得率)が感染確率への免疫効果の因子になります。
赤線の100%の場合、完全燃焼ですから、幅の狭い収束部分をある程度再現できますが、罹患可能人数を85万人と仮定したことに、どの位のリアリティーがあるかが問題です。また、80%、50%の結果が示しているように、少しでも燃焼を免れる人がいると、ピークの収束は急激に弛緩してしまい、鋭いピークアウトは再現できません。
4.ウイルス自滅効果
前回の連載で展開した仮説です。ウイルス自体が変異の重なりで自滅するというものです。シミュレーションでは、ウイルスの自滅を記述するために、ウイルス固有の時間として、世代数を定義して、ある世代になるとウイルスは自滅すると仮定しました。
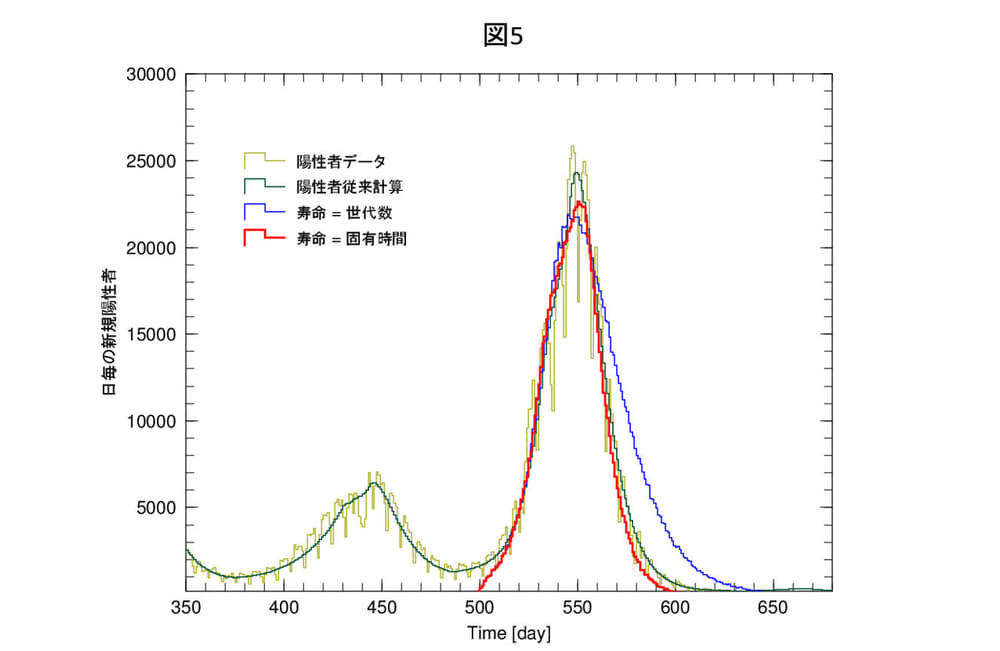
図5の青色の結果が世代数を使った結果で、インドのデルタ株の結果は良く再現できましたが、日本のデルタ株の幅の狭いデータは、事象ごとの世代の時間幅が影響して再現できません。そこで、今回は、ウイルスの持つ固有時間そのものを寿命の判定に用いることにしました。赤線がその結果です。寿命は52日を設定しています。
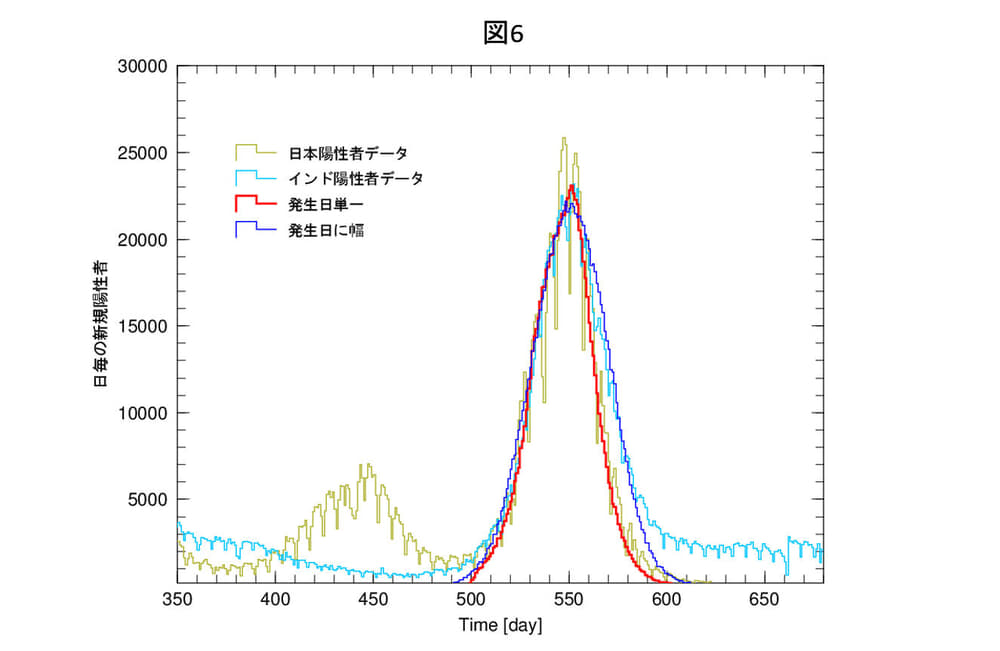
それでは、インドのように少し幅の広いものはどのように記述するかというと、日本場合は、発生日を同じ日にしていますが、インドの場合、発生日に幅を持たせることにより、データを再現することができます。結果を図6に示します。
5.ウイルス自滅+ワクチン効果
ウイルス自滅効果を取り入れたモデルが、ピークアウトの幅をよく再現できることが分り、ピークアウトのメカニズムとしては合格です。ピークアウトのメカニズムが明確になれば、これまでの対策の効果を定量的に評価することができます。例として、ここではワクチン効果の定量的評価を示します。
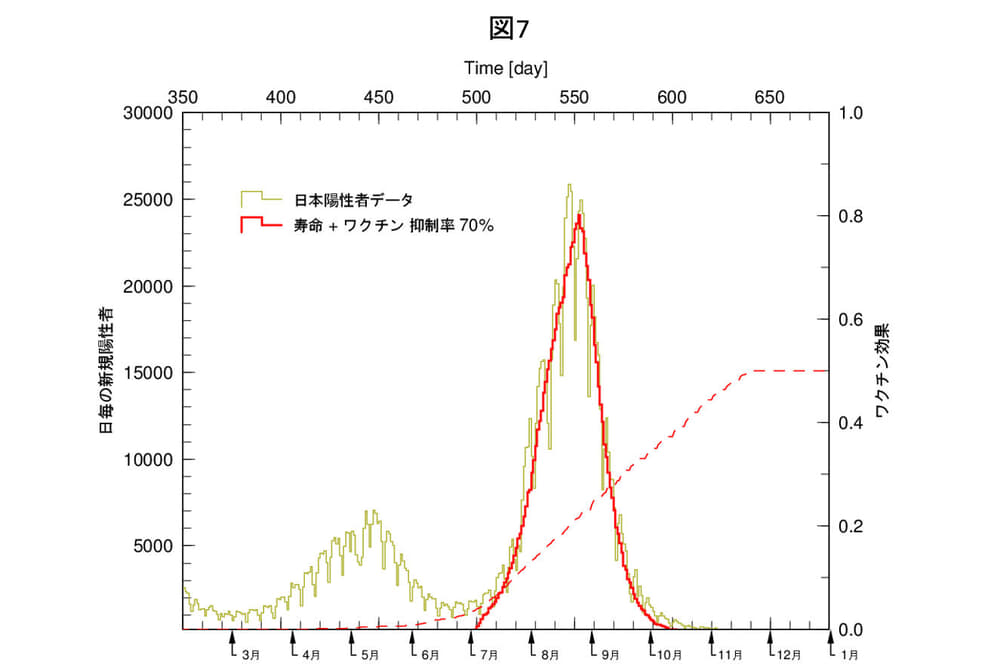
図7は、ウイルス自滅効果とワクチン効果を同時に入れて(ここが重要です)、日本のデルタ株ピークを再現したものです。ワクチンの抑制効果を70%とした場合です。さて、ここからワクチン効果を省きます(これができることがポイントです)。

図8には、ワクチン抑制効果が90%、70%の結果が示してあります。この図よりワクチン効果は、ピーク時の値が、抑制効果90%で5.9倍、70%でも3.9倍あることが分ります。一日の陽性者数が最大2万5千人でしたので、ワクチンがなかった場合、これが10万人から15万人になった可能性があるということが示されます。またワクチンが1ヶ月早く接種されていた場合の効果等を定量的に評価できるようになります。
6.結論
ピークアウトのメカニズムとして、(1) ワクチン効果、(2) 免疫効果(山火事理論)、(3) ウイルス自滅効果、の3つの仮説について、デルタ株のピーク幅に注目して検証しました。ワクチン効果、免疫効果ではデルタ株収束部の狭い幅を再現できず、ウイルス自滅のシナリオを採用することによって初めてこの狭い幅を再現することができました。
ピークアウトのメカニズムが明確になれば、ワクチン効果やこれまでの対策の効果を定量的に評価することができますし、ピークアウトのメカニズムを解明できなければ、これまでの対策の効果の評価はできないということです。
本稿で行ったことは、ある仮説に基づくシミュレーションですので、その仮説自身の実験とデータに基づく更なる裏付けが必要です。シミュレーションと違って、これらの研究は実際の「物」がある世界ですので、今後の発展を大いに期待できます。














