
goleiro35/iStock
(モンテカルロシミュレーションで検証 連載38)
山本和生氏のアゴラ記事「コロナウイルスの自己破壊を説明する2つの仮説」は、待ちに待った仮説です。1年以上、モンテカルロシミュレーションを用いて、コロナ感染拡大の現象を解析してきましたが、ピークアウトのメカニズム、各国のピークの半値幅等の共通性、ピーク後の収束時の一様性等は、3密回避、人流抑制、ロックダウン等の人間側の対策の効果としてはどうしても解釈できないと感じていました。
これらに対して、コロナウイルス自己破壊、即ち、コロナウイルスに寿命があると仮定すると、これまでの現象論的な解析が、非常に整合性の取れた解析になるということを本稿で示します。
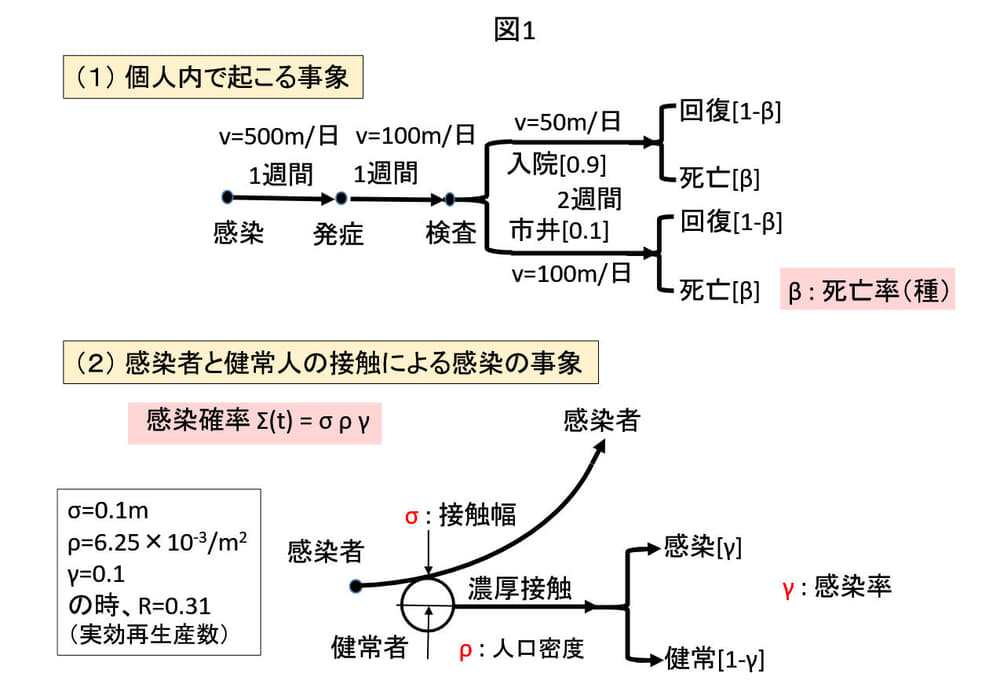
図1は、本シミュレーションに取り入れているプロセスです。プロセスは2つ、ひとつは、感染から発症、検査入院、回復もしくは死亡という個人内で起きるプロセス、もうひとつは、感染者と健常人が接触して新たな感染が引き起こされるプロセスです。シミュレーションで実際のデータを再現するときに動かしているパラメータは、(1)のプロセスでは死亡率、これは、本シミュレーションで導入している「種」毎に変化させ、「種」内では一定にしています。
感染拡大収束を制御しているパラメータは、(2)のプロセスの感染確率Σ(t)=σργです。このパラメータを、データを再現するように時間の関数として変化させます。Σは3つのパラメータの積として表されています。σは接触幅、2次元でやっているので幅ですが、3次元だと断面積です。どのくらい近づけば人と人は接触するのかというパラメータで、ソーシャルディスタンス等の効果に対応するパラメータです。
ρは、人口密度です。SIRモデルで言うと、感染可能な人の密度です。ここに3密になった効果、また、免疫を持った人の効果等が入ります。γは、感染者と健常人がσの幅以内で接触した時の感染率です。マスクの効果、ワクチンの効果等がここに入ります。
実際の感染拡大収束を再現するように、Σ(t)を動かすのですが、ピークアウトを記述しようとすると、ある時点で突然、Σの値を1/4くらいに減少させることが必要になります。1/4減少というと人流の75%減少に対応します。西浦氏によれば「接触8割削減すれば収まる」ということでしたが、確かにシミュレーションでは8割Σが減少すればピークアウトします。しかしながら、ピークアウトが起こった時に、現実社会でσ、ρ、γに対応するような、例えば人流の急激な変化や、ワクチン接種率の急激な増加はこれまで観測されていません。
それでも実際の人流の変化等は、穏やかであっても感染拡大に現れているはずです。両者の関係を注視すれば何がしかの相関が見られるはずです。ところが、ピークアウト後の収束期では、現在の日本がそうですが、ピーク後の指数関数的減少が始まると、ほとんどの場合、人的な変化に関係なく減少します。
この2点に加えて、第1波の時に解析しましたが、世界各国コロナ対策はまちまちであるにも関わらず、各国のピークの半値幅が一致しています。どうしても、人間側の問題でなく、コロナウイルス側の特質が関係しているのではないかと考えた理由です。
さて、山本和生氏のコロナウイルスの自己崩壊の仮説を取ると、これらの問題に対して整合性の取れる結果が出るのか、シミュレーションで検証してみました。
シミュレーションでは、個々の感染の事象をイベントとして記述できていますので、まず、ウイルスの世代と寿命を定義しました。感染者が他人に感染させると、感染させた人のウイルスの世代がひとつ進み、感染者のウイルスもその世代数を引き継ぐ、そしてウイルスはある世代になると感染能力がゼロになるという仮定です。感染確率にウイルス側のGn(nは世代数)という因子が加わります。
Σ(t)=σργ×Gn (1)
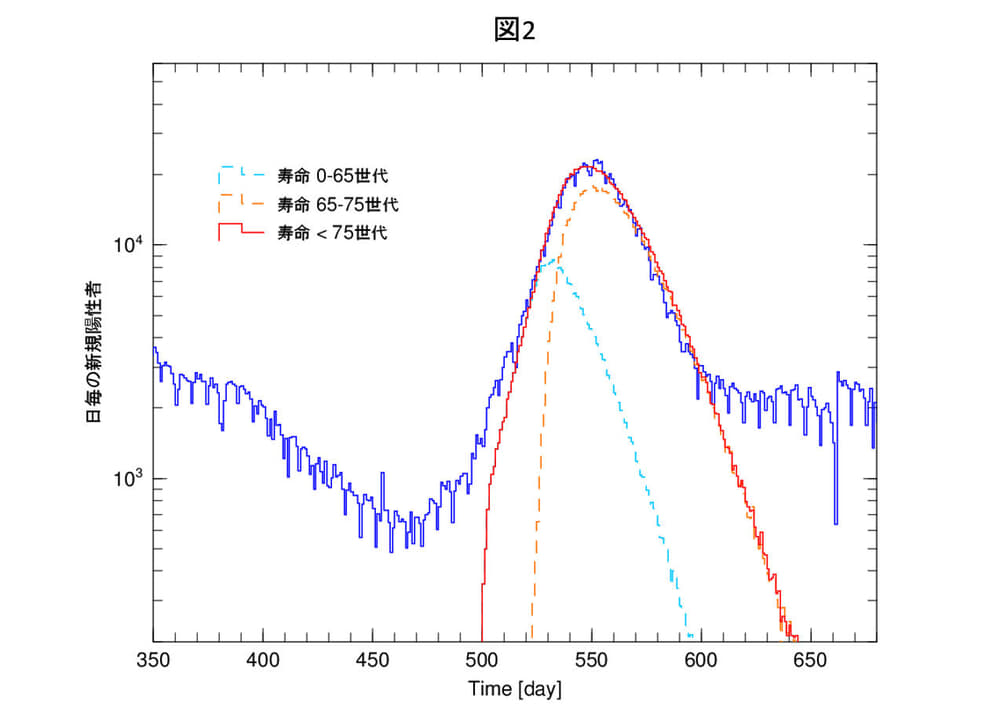
図2は、インドのデルタ株のピークをウイルスの寿命を使ったシミュレーションで再現したものです。デルタ株のウイルスの寿命を75世代としました。破線は、世代が65世代以前と以後に分けたものです。この場合、感染確率Σ(t)のうち、σργはピークの前後で一定で、ウイルスの寿命の項Gnでピークアウトします。
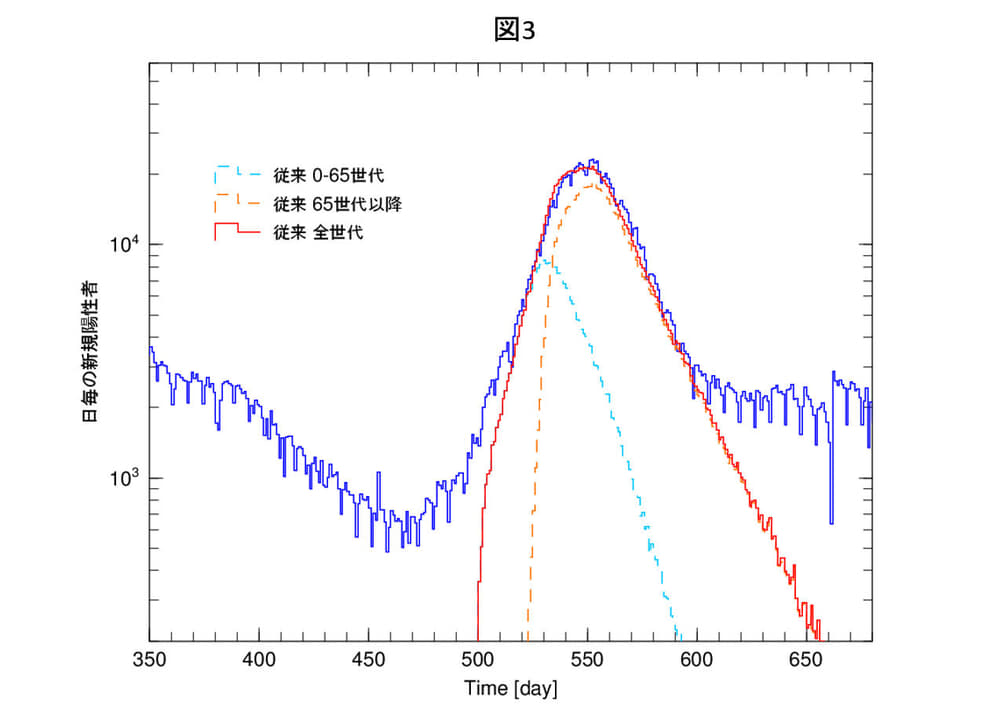
図3は、同じ問題を従来法で計算したものです。この場合、感染確率Σ(t)のうち、寿命の項Gnは一定で、σをピーク前でσ=0.83で図2と同じ、ピークアウト時にσ=0.20とほぼ1/4にして収束させています。破線は65世代までの寄与と、それ以後全世代の寄与です。従来法の場合は、ピーク以後の世代の寄与を、強制的にσを小さくして収束させていることになります。
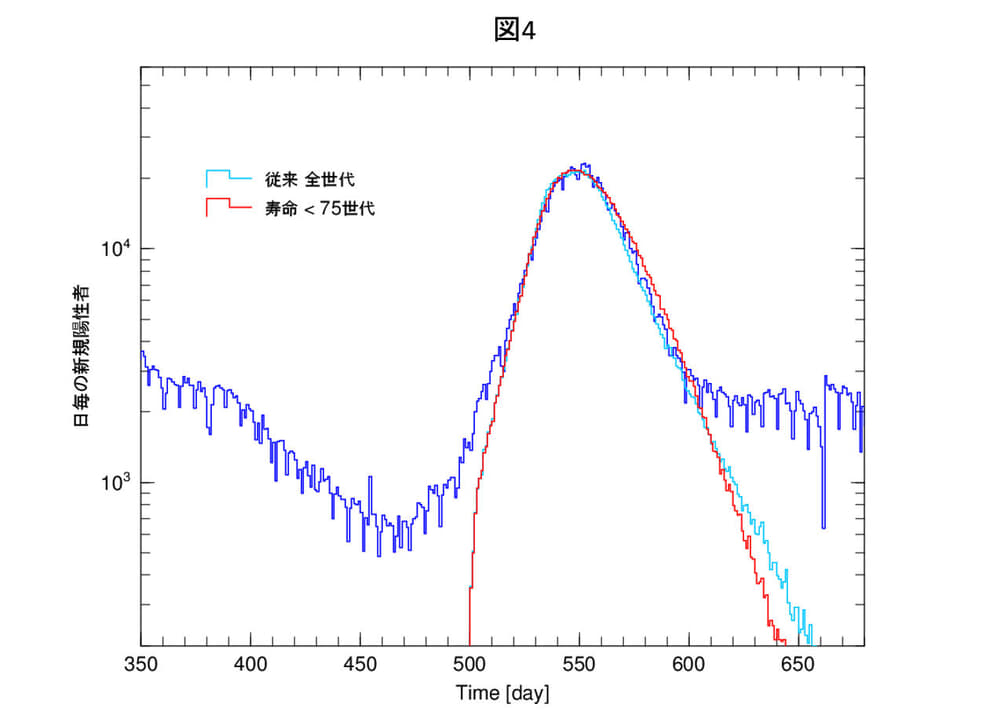
図4は、従来法と寿命を使った方法の結果を比較したものです。ほぼ同等の結果が得られます。これは、これまでの解析で用いてきたピークアウトを記述する手法、即ち、感染確率Σ(t)のうちσργをピーク時に変化させるという方法は、寿命の項Gnを導入することにより、自動的に記述できるということ、また逆に、これまでの方法は、近似的に寿命の項Gnをσργに取り込んだ手法で、ほぼ同じ結果を再現できることを示しています。
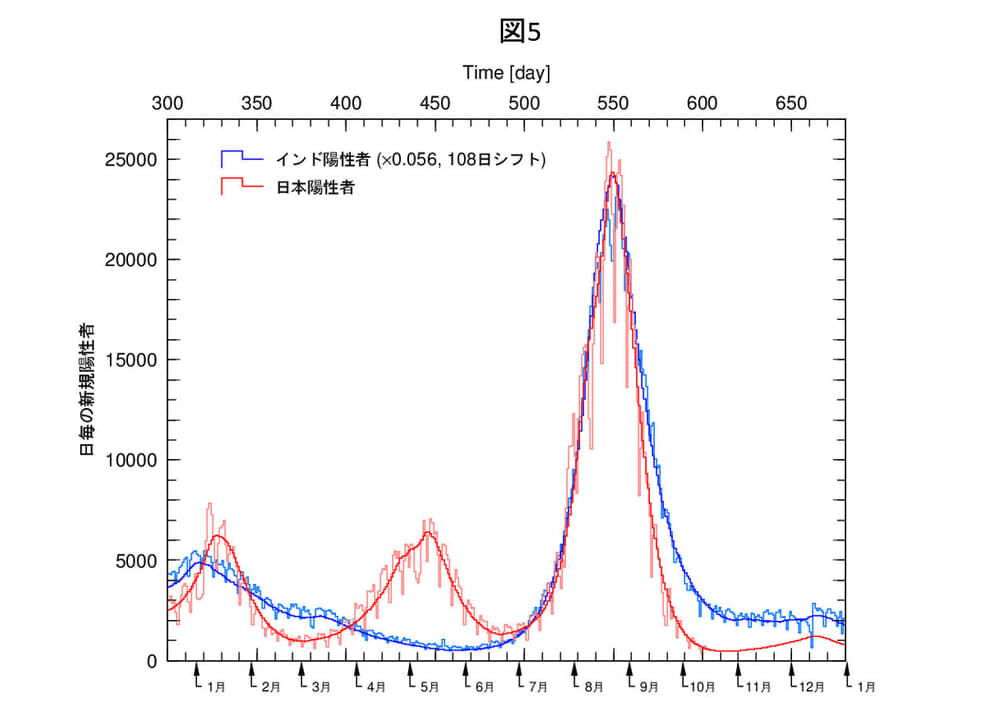
図5は、日本とインドのデルタ株を、ピーク位置を規格化して比較したものです。同じデルタ株で、ピークを形成し収束していますが、収束部に差が出ています。おそらく、日本の場合、ワクチン接種の急激な普及が原因だろうと思われますが、寿命による収束部分が共通であるとすれば、ワクチン効果の詳細の評価ができると期待できます。
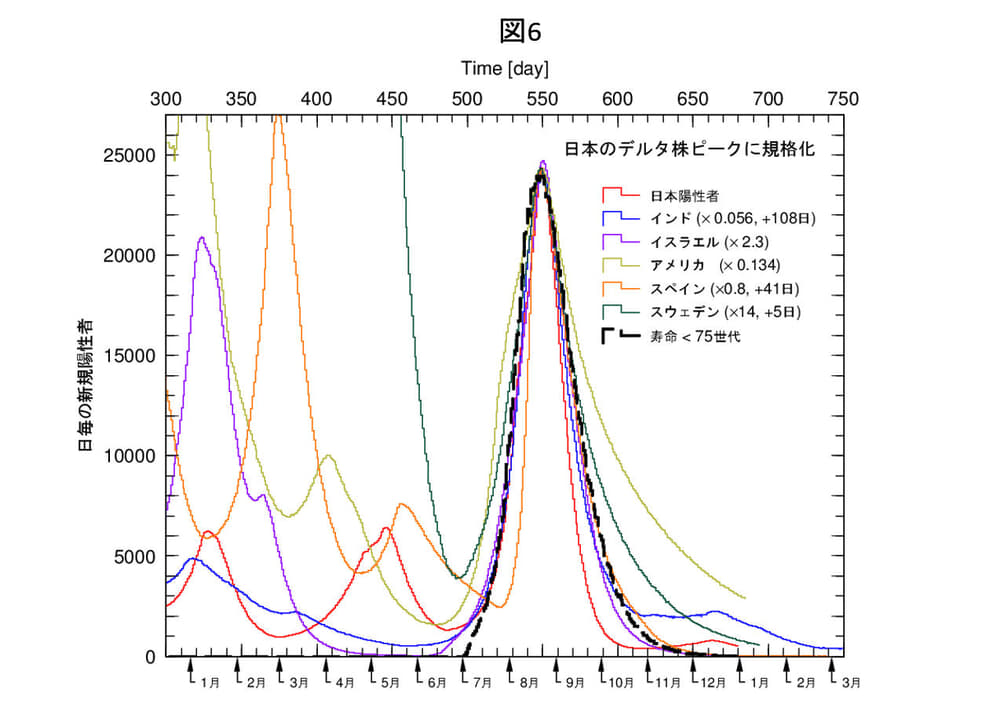
図6は、日本、インドの他に解析を行っている国で、デルタ株でピークを作っている4カ国を加えました。第1波ほどではありませんが、同じようなピークを形成しています。ウイルスの寿命を仮定すれば、黒太破線で示したように共通部分が記述できます。ここからの差が各国の対策の違い等に帰結できるはずです。
結論
ウイルスの寿命を仮定すれば、これまで感染確率を変化させることによって記述してきたピークアウトは、寿命の性質から自動的に導出されることになります。また、ピークアウト後の人流等に影響されない収束も説明できますし、世界各国に見られる同じ株の共通性も説明できます。
ピークアウトの主たるメカニズムがウイルスの寿命であるとすると、人流の抑制等の対策の効果は非常に限定的である可能性が強い。図5,6で示したような方法で、ウイルスによる変化と対策による効果を分離し、これまでの対策の定量的な評価が望まれるところです。














