
zhuyufang/iStock
(モンテカルロシミュレーションで検証 連載42)
日本の第5波(デルタ株)について、緊急事態宣言による人流抑制の効果を定量的に評価します。多くの人に犠牲を強いた人流抑制の数々の施策は、その効果を定量的に評価されないまま現在に至っています。今後、同様な施策を打ち出すには、明確な評価を基礎とした説明が必要とされます。その例となるものを示します。
まず、人流抑制の施策によって、局所的に人の密度が急激に変化するもの(夜の街、飲食等での感染)をAとします。残りは、人流抑制の施策によって基本的に変わらないもの(家庭内人数、施設内人数)をBとします。そしてA / (A+B)を50%と仮定した場合、第5波(総陽性者数85万人)の人流抑制の効果を定量的に解析した結果は以下の通りです。
- 人流抑制政策によって陽性者数の増加は抑えられ、その効果は49%、42万人の陽性者抑制であった。
- 人流抑制の効果は、ピークアウト後の新規陽性者に対しては全くなかった。
- 緊急事態宣言の開始時期が重要で、12日の前倒しで陽性者は26%、22万人の減少、10日の遅延で19%、16万人の増加となった。
解析の手法は、ワクチンの効果を評価した連載40(日本のワクチン接種の成果)の方法と同じ。ポイントは、ピークアウトのメカニズムとワクチン効果、人流抑制の効果等を分離できることです。従って、緊急事態宣言を出す時期を早めた場合、遅かった場合など、現状を再現した時と同程度の精度で評価することが出来ます。定量評価を目的とします。
1.人流変化の定量化
人流変化をモデル化するに際して、本稿では次のデータと仮説を用います。
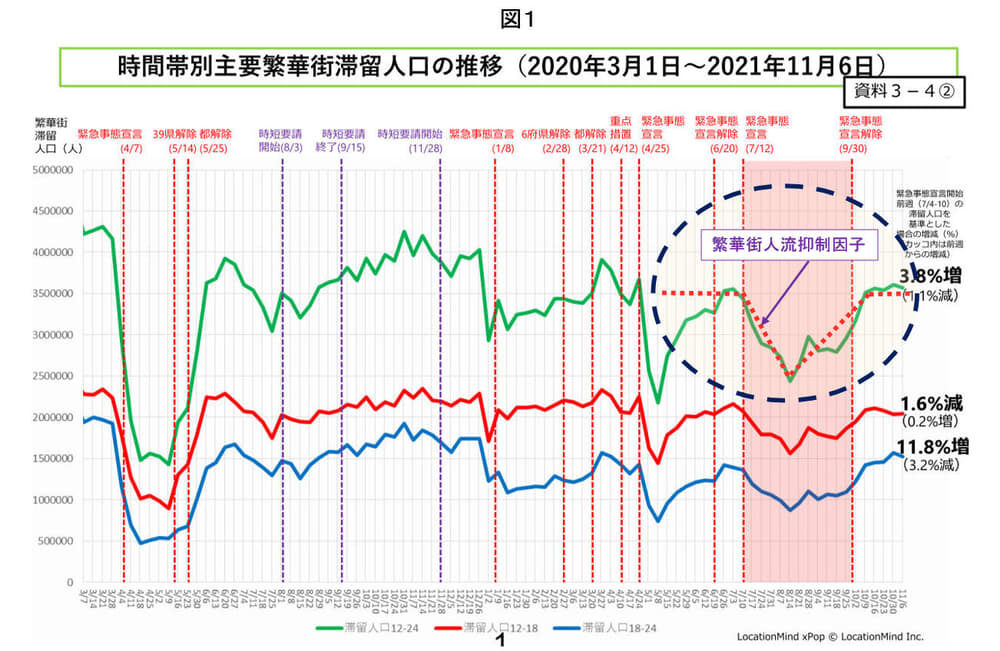
図1は2021年11月9日のアドバイザリーボードの資料にある、繁華街の滞留人口の推移のデータです。この中から、破線の楕円で囲んだ部分に注目し、緑線の滞留人口の推移を簡略化した赤点線の関数を人流抑制因子のデータとして使います。7月12日からの緊急事態宣言の日から、8月15日まで30%減少し、10月10日まで再び上昇し、7月12日と同じレベルに戻るという設定です。
実際のシミュレーションの中では、この人流抑制因子は各々の感染確率にかかる係数です。ここでは、全体の50%が人流変化に連動する感染と仮定しますから、上の例の30%は、全人口で平均すると最大15%の変化になります。
これまでの連載と同じ方法で、ワクチン効果、人流効果、ウイルス自滅効果を入れたモンテカルロシミュレーション用い、第5波のピークを再現するように、感染確率のパラメータを決めます。ここでは「人流変化に連動する感染」の割合を50%と仮定しましたが、この仮定は過去のデータを再現するという条件で検証されます。その上で、それぞれの効果を外す、もしくは、移動することによって、それぞれの効果を評価します。
2.人流抑制の効果
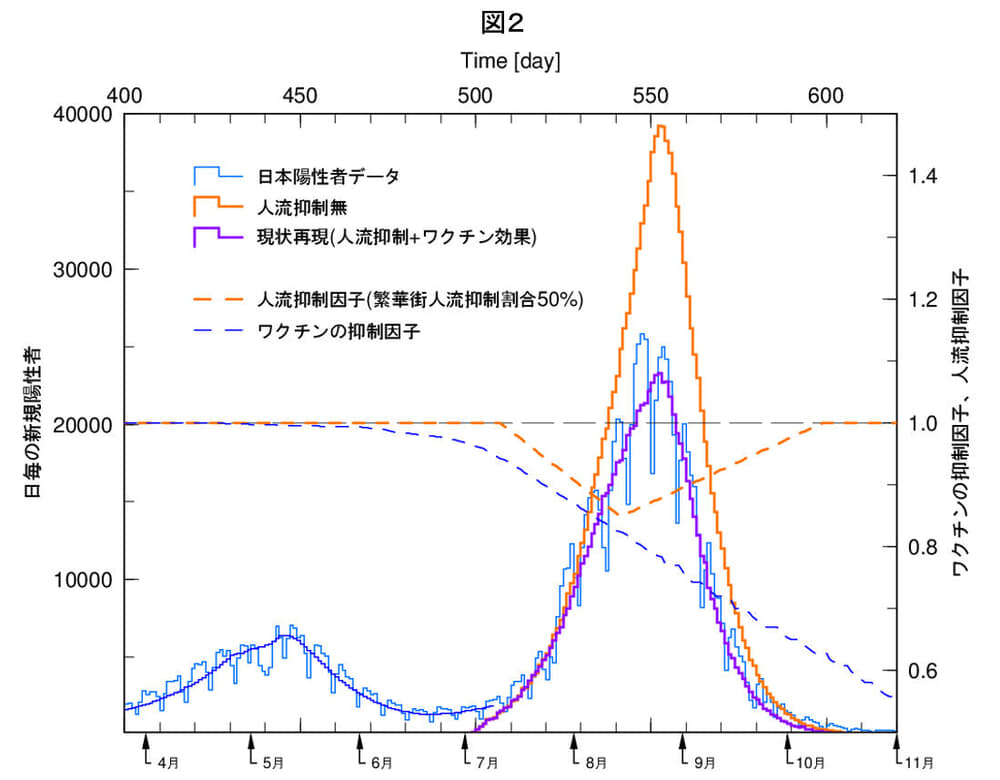
図2には、陽性者の日毎変化と共に、計算で用いたワクチン効果の抑制因子(青破線)、人流抑制効果の因子(橙破線)を表示(右側の目盛)しています。この両因子を入れて、陽性者データを再現したのが紫線です。さて、ここからがシミュレーションの特色ですが、この状態から、橙破線の人流抑制因子を1にします。つまり人流抑制効果をゼロとします。結果は橙色の実線です。この差が人流抑制の効果で、陽性者数で33%、42万人の抑制です。
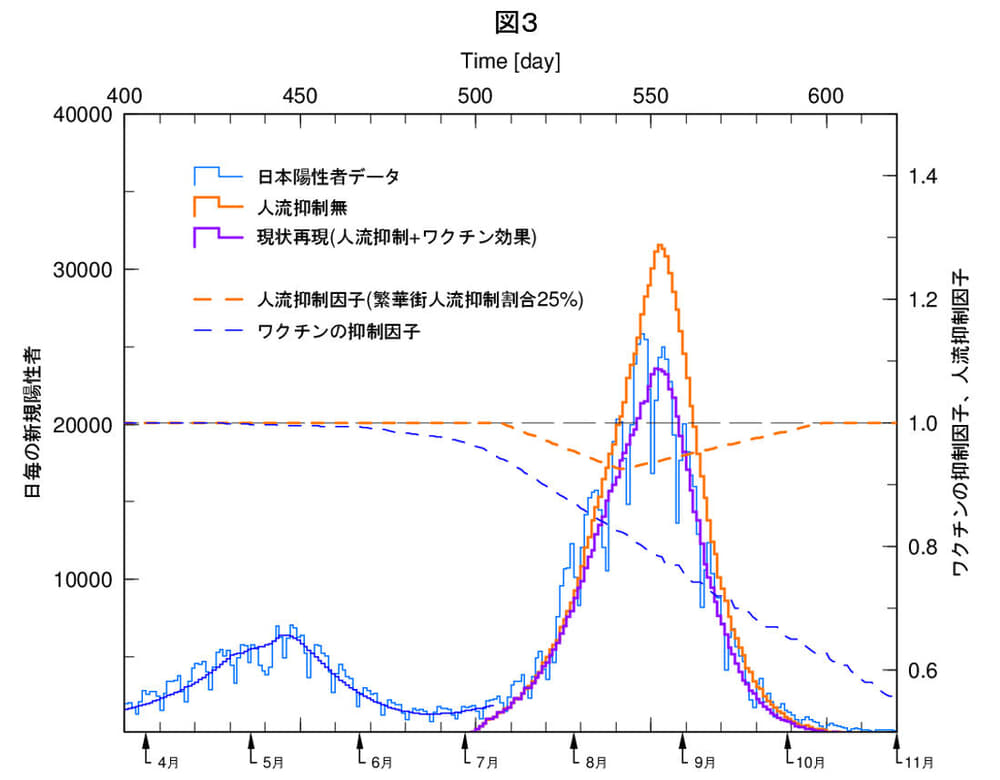
図3は、「人流変化に連動する感染」の割合を25%とした場合の結果です。図2の50%の結果と比較すると、人流抑制効果は陽性者数で25%、21万人の抑制となります。これらは50%の時の約半分となり、ほぼ「人流変化に連動する感染」の割合に比例します。従って、このパラメータの依存性は強いので、「人流変化に連動する感染」の割合は、別種のデータからより詳細に検証されるべきパラメータです。
3.ピークアウト後の収束と人流拡大の関係
デルタ株の第5波は、人流データは増加を示しているにもかかわらず、ピークアウト後は急激に陽性者が減少し、現在に至っています。この事実から、これまで感染拡大収束には、人流抑制の効果は全く寄与していないのではないかという仮説まで出ていましたが、これは妥当ではないということが図2、図3でわかります。
では、どうしてピークアウトの後は人流の変化に左右されないのか。これは連載38、連載39で示したように、ピークアウトを決定づけているのは、コロナウイルス側の問題(寿命のようなメカニズム)であると考えられるので、これをモデル化しました。
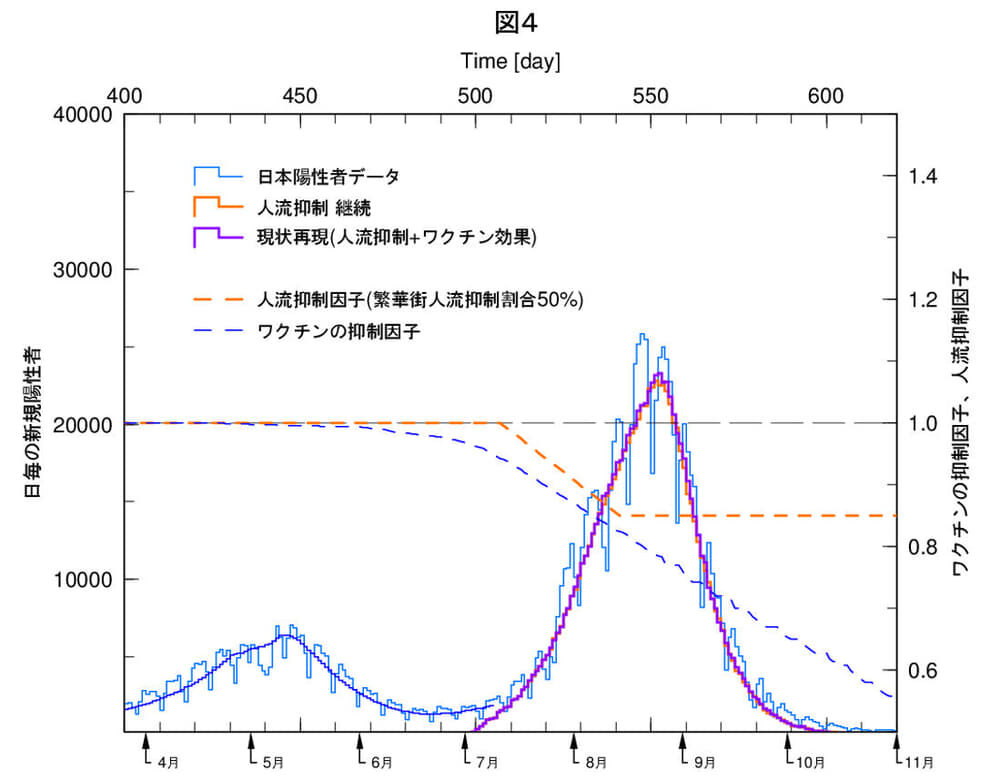
例えば、このモデルで8月15日からの人流の増加をさせず、抑制が継続したものと仮定します(橙破線)。図4がその時の結果です。橙色の抑制因子を8月15日以降継続させても、陽性者数の推移は全く変化しません。
4.人流抑制の開始時期
この事実は、人流抑制の施策が、ピークアウト後はほとんど影響を及ぼさず、ピークアウト前の開始時期が特に重要であることを示唆しています。そこで、開始時期の依存性を検証しました。
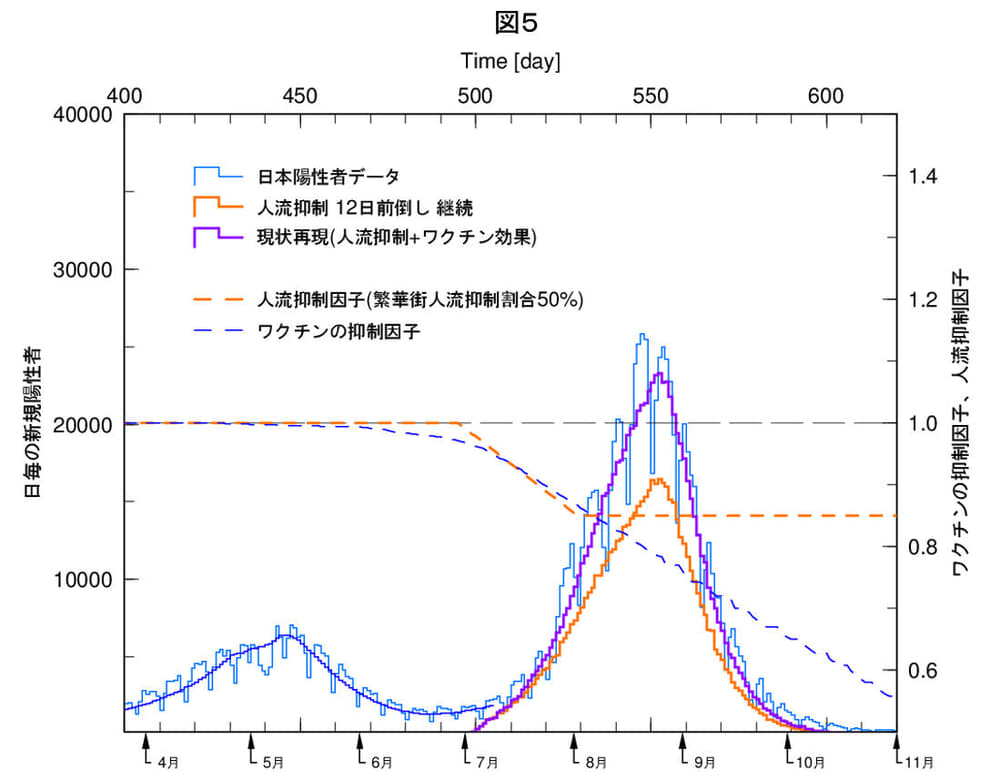
図5は、図4の条件で、開始時期を12日前倒しした場合の結果です。陽性者数は現状に比べて26%、22万人の減少です。
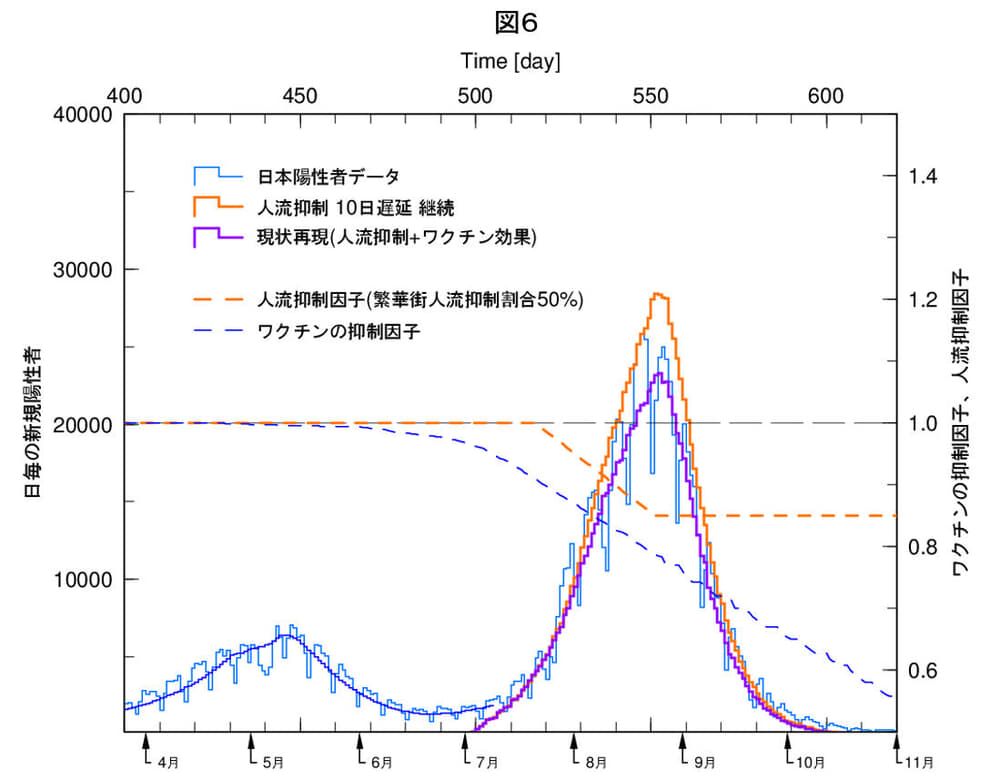
図6は、逆に図4の条件で、開始時期を10日遅延させて場合の結果です。陽性者は現状に比べ19%、16万人の増加です。
5.結び
「急激な感染拡大を見て、人々の行動変容が起こった」というのは、検証不可能な表現ですから、まず検証可能なモデルを作り、過去のデータと比較し、その妥当性を評価できなければなりません。今後、同様な施策を打ち出すには、明確な評価を基礎とした説明が必要とされます。














