skodonnell/iStock
コロナワクチンの予防効果(有効率)は、コホート研究により算出されています。これは、接種群と未接種群を追跡調査して感染の有無を調べる研究方法です。信頼性の高い研究方法ですが、大きな短所があります。研究にかかる労力や費用が莫大なのです。
そのため労力と費用が莫大ではなく信頼性が比較的高い研究方法として、診断陰性例コントロール試験が開発されました。実は、近年のインフルエンザワクチンの有効率は、ほとんどこの手法を用いて報告されています。コロナワクチンの報告でも、この手法を用いた論文が発表されるようになってきました。今後、日本でもこの手法を用いた発表が増加することが予想されます。
この研究方法のユニークな点は、コントロール群を病院受診者のうち検査陰性者とした点です。この設定により、受診行動バイアスの補正を考えなくてもよくなりました。
これは、感染症状が生じた場合、病院を受診して検査を受ける確率は、 接種者と未接種者では異なる可能性があるというバイアスです。感染症状があればすぐに病院を受診する人もいれば、薬局で薬を買って様子をみる人もいれば、軽症であれば何もしないという人もいたりするなど、症状が生じた後の行動は、人により様々という話です。コホート研究において、この受診行動バイアスの補正は決して簡単ではありません。
診断陰性例コントロール試験は、なかなか優れた研究方法なのです。では、コロナワクチンでも初めからこの研究方法を用いればよかったのではないかという疑問が生じてきます。実は、この研究方法のロジックは、コホート研究のそれと比べると少々トリッキーなのです。今回の解説の主題は、このロジックを考察することにあります。
まず、ワクチン有効率研究の定石であるコホート研究においての計算式を見てみます。
ワクチン有効率=1 - 接種群の感染率 ÷ 未接種群の感染率
医療統計学の用語のリスク比を用いますと、次の式となります。
ワクチン有効率=1 - リスク比
感染率がリスクであり、その比率がリスク比となるわけです。この式の意味が、分かりにくいと感じる方は、 こちらの解説 をご覧ください。
一方、診断陰性例コントロール試験では、ワクチン有効率は次の式より計算されます。
ワクチン有効率=1- オッズ比
オッズという新たな指標が登場しました。オッズを用いたロジックは、独特であり、簡単には理解できません。具体例を挙げて説明してみます。
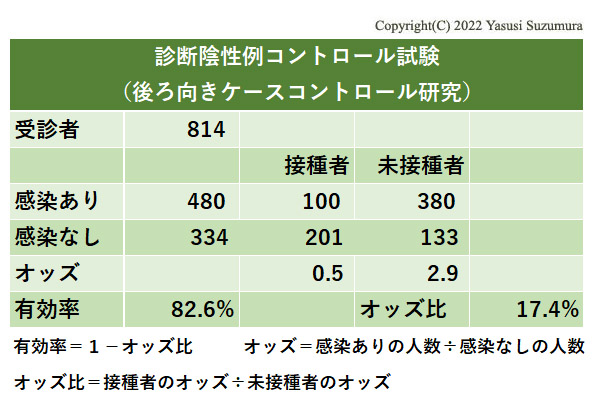
ある病院に、感染症状を有する患者が814人受診し、新型コロナ感染症の検査したところ陽性者(感染あり)が480人、陰性者(感染なし)が334人であり、その際にワクチン接種の有無を確認したところ、上の表のようになったとします。検査陰性者(感染なし)とは、新型コロナ以外の感染症に感染して受診した人です。
接種者の感染者は100人ですが、コホート研究のように追跡調査をしたわけではないため、感染率を計算することはできません。そこでオッズというものを計算します。オッズは、感染ありの人数を感染なしの人数で割った数値です。更にオッズ比を計算して、1よりオッズ比を引いた数値を求めます。 診断陰性例コントロール試験では、この数値82.6%がワクチン有効率ということになります。
理解できたでしょうか?
私は初めてこの説明を読んだ時、さっぱり分かりませんでした。論理が飛躍しているとしか思えません。しかし、この手法がインフルエンザワクチンの有効率を調べる時の定番となっているのは事実なのです。
医療統計学では、イベント発生率(感染率)が低い場合には、オッズ比はリスク比に近似すると考えます。つまり、感染率が低い時、リスク比はオッズ比で代用できるわけです。そして、このことが診断陰性例コントロール試験のロジックの根幹になっています。
では、本当に正しいワクチン有効率を計算したことになっているのかを検証してみることにします。
架空の前向きコホート研究を想定します。接種群6万人、未接種群4万人で追跡調査をして、感染者が接種群では100人、未接種群で380人となったとします。有効率は82.5%となります。
次に、このデータを診断陰性例コントロール試験により後ろ向きに見てみます。受診してから、過去の接種歴を確認しますので後ろ向きなのです。感染ありの人数は、そのまま使用します。感染なしとは、新型コロナ以外の感染症で受診した場合です。その人数の設定は難しいですが、新型コロナの受診率(480/100,000)の7割とひとまず設定します。有効率にほとんど差がなければ、診断陰性例コントロール試験は信頼できる研究方法ということになります。
感染率が低い場合に、オッズ比はリスク比に近似するとされていますので、3つの感染率で検証してみます。
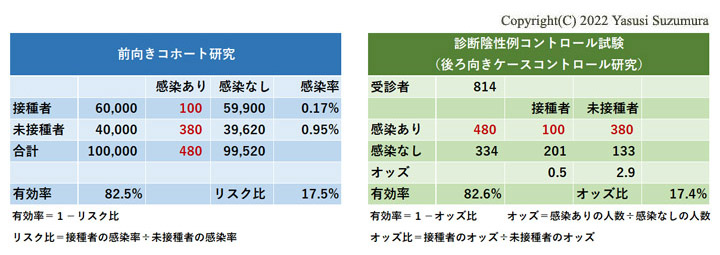
有効率は、ほぼ同じです。差はわずかに0.1%です。
感染者を10倍に増やして有効率を比較してみます。
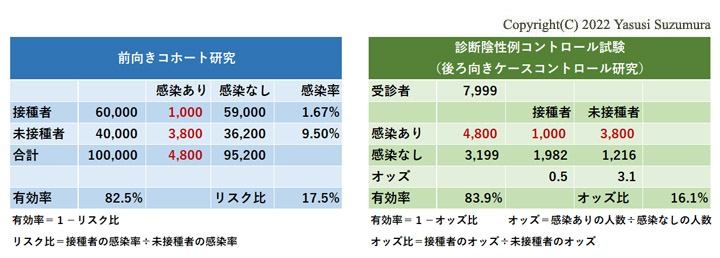
有効率は、ほぼ同じですが、差は1.4%に増加しました。
感染者を100倍に増やして有効率を比較してみます。
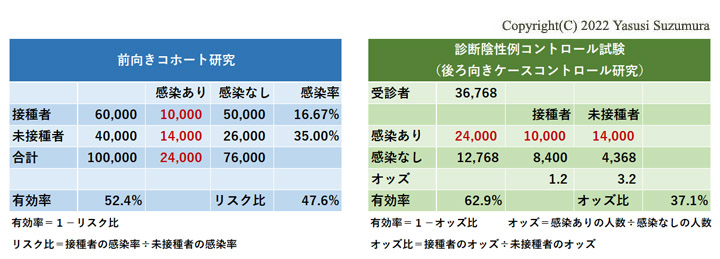
有効率の差は、10.5%に増加しました。
感染率が低い数値であれば、診断陰性例コントロール試験で得られた有効率は信頼できることが分かりました。
最後に数式を用いて、なぜ感染率が低い時に、リスク比がオッズ比で代用できるのか考察してみます。数値を変数に置き換えます。受診率をpとしましたが、オッズ比を計算する時に相殺されますので、pの値に意味はありません。
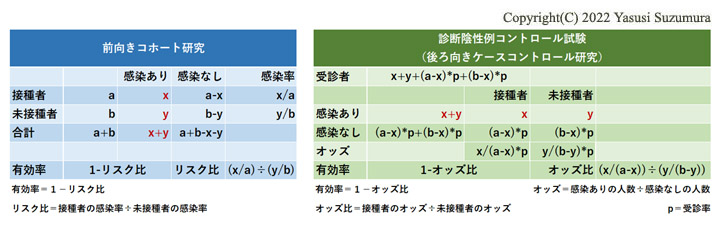
リスク比をオッズ比で代用するには、リスク比をオッズ比で割った数値が1に近似している必要があります。 式で表すと次のようになります。
((x/a)÷(y/b)) ÷ ((x/(a-x))÷(y/(b-y))) ≒ 1
括弧をはずして式を整理してみます。括弧内を先に演算するという数学の規則を破ることになりますが、整理しないと分かりにくいのでここは妥協します。
(b/a) ÷ ((b-y)/(a-x)) ≒ 1
式が成立するためには、xとyが、aとbより十分に小さいことが必要だということが分かります。つまり、感染率が十分に低ければ、リスク比はオッズ比で代用できることになります。ただし、感染率がどの程度低ければ代用可能かについてのルールは存在していません。実際の研究では、代用には限界があることを理解した上で、計算することが大切と言えます。
【補足】
診断陰性例コントロール試験では、何らかの症状が生じて病院を受診した人が対象ですから、 無症状の感染者を捕捉することはできません。 したがって、発症予防効果(有効率)と重症化予防効果(有効率)は検証できますが、 感染予防効果(有効率)は検証できません。